Общие условия перехода от дозвукового течения к сверхзвуковому и обратно

Ранее было показано, что при подводе теплоты или совершении работы трения в движущемся по цилиндрической трубе с дозвуковой скоростью газе происходит увеличение числа Маха. Такое же явление наблюдается в дозвуковом потоке при течении без теплообмена и трения в суживающейся трубе.

Изменение числа М в газовом потоке происходит также при изменении расхода газа в канале и при совершении механической работы. Указанные воздействия вызывают изменение числа М как в дозвуковом, так и в сверхзвуковом потоке газа.

Рассмотрим влияние этих воздействий на скорость движения газа. Для простоты будем считать газ идеальным.

Массовый расход газа определяется выражением

.

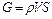Дифференцирование этого уравнения и последующее почленное деление результата на массовый расход дает следующую зависисмость:

.

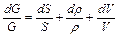Дифференцируя уравнение состояния идеального газа (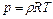), получаем

,

или

.

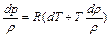Использование вышеприведенных выражений дает

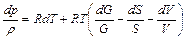. (2.62)

Из уравнения Бернулли в дифференциальной форме имеем

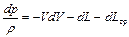, (2.63)

где L – удельная техническая работа; 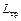– удельная работа трения.

Сопоставляя (2.62) и (2.63), а также освобождаясь от членов, содержащих плотность и давление, получим

.

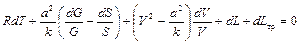Здесь используется выражение для скорости звука ().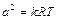

От члена, содержащего температуру (RdT), можно избавиться с помощью дифференциального уравнения энергии (первого закона термодинамики для потока)

,

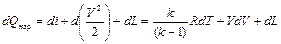где 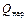– удельная теплота, подводимая к газу извне; 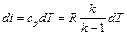– изменение энтальпии.

Производя элементарные преобразования, приходим к соотношению, связывающему изменение скорости газового потока с внешними воздействиями (геометрическим, расходным, механическим, тепловым и трением):

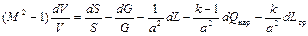. (2.64)

Это соотношение было установлено Л. А. Вулисом и получило название «условие обращения воздействия». Особенность этого соотношения состоит в том, что знак его левой части изменяется при переходе скорости через критическое значение. Поэтому характер влияния отдельных физических воздействий на газовое течение противоположен при дозвуковом и сверхзвуковом режимах. Воздействия, вызывающие ускорение в дозвуковом потоке (сужение канала 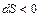, подвод дополнительной массы газа 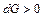, совершение газом работы 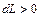, трение и подвод теплоты 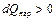), приводят к замедлению сверхзвукового потока. Воздействия обратного знака (расширение канала 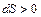, отсос газа 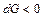, сообщение газу механической энергии 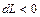и отвод теплоты 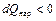) приводят к замедлению дозвукового и ускорению сверхзвукового потоков. Отсюда следует важный вывод, что под влиянием одностороннего воздействия величину скорости газового потока можно довести только до критической, но нельзя перевести через нее. Например, путем подвода теплоты можно ускорять дозвуковой поток, но только до тех пор, пока не получится М = 1. Для того чтобы перевести дозвуковой поток в сверхзвуковой, нужно переменить знак воздействия, т. е. в зоне М = 1 начать отводить теплоту.

Подогрев газа в сверхзвуковом течении вызывает торможение потока, но переход к дозвуковому течению и дальнейшее торможение станут возможными только в том случае, если, начиная с М = 1, мы переключимся на охлаждение газа.

Ускорение газового потока в сопле при любой комбинации воздействий требует достаточного перепада давлений между сечениями, расположенными перед и за соплом.

Рассмотрим раздельно каждое из четырех воздействий.

При этом получим в дополнение к общеизвестному способу получения сверхкритических скоростей с помощью сопла Лаваля еще три, указанных Л. А. Вулисом, способа перехода через скорость звука – с помощью расходного, механического и теплового сопел.

Сопло Лаваля, представляет собой канал, в котором только за счет придания ему соответствующей формы можно осуществить переход от дозвуковой скорости к сверхзвуковой. В этом частном случае чисто геометрического воздействия на поток (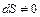) отсутствуют прочие воздействия, ().

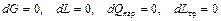Но тогда соотношение (2.64) переходит в полученное ранее равенство:

.

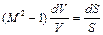Ускорение потока в дозвуковой части сопла Лаваля (М < 1) получается путем сужения канала (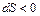). Однако, начиная с критического сечения (М = 1), для получения сверхзвукового потока и дальнейшего его ускорения приходится изменять знак воздействия, т. е. расширять канал ().

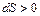Течение идеального газа в геометрическом сопле при отсутствии трения является изэнтропическим. В критическом сечении (М = 1) сопла воздействие проходит через минимум ().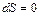

Расходное сопло дает возможность получить переход через скорость звука за счет изменения расхода газа в трубе постоянного поперечного сечения (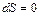) при отсутствии обмена с внешней средой работой (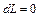) и теплотой (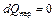) и при течении без трения (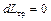). В этом случае соотношение (2.64) принимает следующую форму:

.

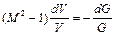Ускорение движения (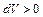) достигается здесь за счет подвода дополнительной массы газа в дозвуковой части канала и отсоса газа в сверхзвуковой его части. В критическом сечении (М = 1) расход газа и, следовательно, плотность тока проходят через максимум.

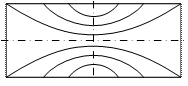Расходное сопло в принципе аналогично геометрическому. Если разбить поток в расходном сопле на отдельные струйки постоянного расхода, то каждая из них представляет собой геометрическое сопло с наиболее узким сечением в области кризиса (М = 1). Однако сужение элементарных струек в нем осуществляется не путем сужения общего канала, а за счет подвода и отвода дополнительных количеств газа (схема течения в расходном сопле представлена на рисунке).

Изменение состояния идеального газа в расходном сопле (без трения) происходит изэнтропически.

Механическое сопло предоставляет еще один возможный способ перехода через скорость звука: за счет технической работы при отсутствии других воздействий ().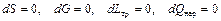

В этом случае основное соотношение (2.64) выглядит так:

,

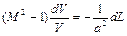Из него следует, что если движущийся газ совершает работу (dL > 0), например, в турбине, то дозвуковой газовый поток (М < 1) ускоряется (dV > 0), а сверхзвуковой (М > 1) – замедляется (dV < 0).

При подводе работы (dL < 0), например, с помощью лопаток компрессора, к газу при дозвуковом его течении наблюдается замедление потока, а в случае сверхзвукового течения – ускорение.

Непрерывный переход через скорость звука в механическом сопле получается при изменении знака воздействия в критическом сечении. В принципе, пропуская дозвуковой поток газа через турбину, можно разогнать его до критической скорости; после этого нужно пустить его через компрессор, и тогда получится ускоряющийся сверхзвуковой поток (схема механического сопла изображена на рисунке).

Таким образом, сверхзвуковое механическое сопло должно состоять из последовательно включенных турбины (в области М < 1) и компрессора (в области М > 1), между которыми располагается критическое сечение (М = 1).

Особенностью механического сопла является то, что параметры торможения проходят в его критическом сечении через минимум. В самом деле, уравнение энтальпии для механического сопла можно записать следующим образом:

.

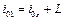Здесь 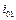, 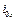– значения энтальпии заторможенного газа соответственно в начальном и произвольном сечениях сопла, L – техническая работа, совершенная газом между начальным и произвольным сечениями сопла. Поэтому в дозвуковой части механического сопла, где газ совершает работу L _т (на турбине), т. е. L > 0, энтальпия (и температура торможения) убывает .

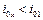В сверхзвуковой области, где к газу подводится компрессором механическая энергия L _к 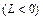, происходит увеличение энтальпии по сравнению с ее значением в критическом сечении:

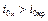или .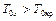

В том, что полное давление и плотность заторможенного газа проходят вместе с температурой торможения в критическом сечении механического сопла через минимумы, можно убедиться и иным способом. Для двух произвольных сечений идеального механического сопла, представляющего собой, по определению, канал постоянного сечения имеем

.

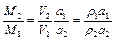Ввиду отсутствия трения и теплоотдачи параметры газа в таком сопле изменяются как при идеальном адиабатическом процессе:

.

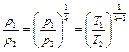Учитывая, что отношение значений скорости звука

,

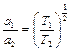получим следующие простые зависимости между значением числа М и параметрами газа в идеальном механическом сопле:

.

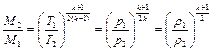Монотонное возрастание значения числа М в механическом сопле сопровождается монотонным падением температуры, давления и плотности.

Кривые изменения параметров потока (рис. а) и торможения (рис. б) в сверхзвуковом механическом сопле при 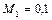и k = 1,4 представлены ниже.

Ошибка! Ошибка связи.

Ошибка! Ошибка связи.

Из предыдущего выражения следует, что максимальная скорость истечения из механического сопла ничем не ограничена

,

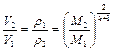так как при 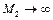имеем 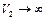. Этот результат связан с тем, что в сверхзвуковом участке механического сопла к газу подводится энергия (dL < 0).

Тепловое сопло, пока еще не осуществленное, дает принципиальную возможность перехода газового потока через скорость звука за счет еще одного – чисто теплового – воздействия при отсутствии других воздействий, т. е. в цилиндрической трубе (dS = 0, dG = 0, dL = 0, dL _тp = 0). Основное соотношение (2.64) применительно к тепловому соплу имеет следующий вид:

.

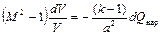Ускорение газа (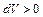) в дозвуковом потоке (М < 1) здесь связано с подводом теплоты (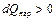), а в сверхзвуковом – с ее отводом (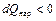). Подвод теплоты при сверхзвуковом и отвод теплоты при дозвуковом режиме вызывают замедление потока (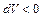). Таким образом, для того чтобы преобразовать дозвуковой поток в сверхзвуковой посредством теплового сопла, на дозвуковом участке последнего нужно повышать энтальпию газа, а на сверхзвуковом – понижать ее. В критическом сечении теплового сопла, где количество подведенного к газу тепла проходит через максимум (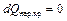), следует изменить знак воздействия.

Температура торможения в критическом сечении теплового сопла (в противоположность случаю механического сопла) достигает максимального значения. Это вытекает из уравнения энтальпии, которое применительно к тепловому соплу имеет следующий вид:

.

Из предыдущего материала, содержащего теорию теплового сопротивления, следует, что при подводе теплоты к газовому потоку полное давление в нем падает, а при отводе теплоты – растет. Формулы теплового сопротивления были выведены применительно к случаю движения газа без трения по трубе постоянного сечения, т. е. именно к случаю теплового сопла.

Из этой теории следует, что полное давление в критическом сечении теплового сопла, как и в механическом сопле, проходит через минимум. Плотность заторможенного газа, прямо пропорциональная полному давлению и обратно пропорциональная температуре торможения, достигает в критическом сечении минимального значения.

В рассмотренных выше идеальных соплах (геометрическом, расходном и механическом) изменение состояния газа было изоэнтропическим, (описывалось уравнением идеальной адиабаты ).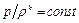

В тепловом сопле в связи с подводом и отводом теплоты энтропия изменяется.

Исследуем термодинамический процесс, который имеет место в тепловом сопле. Дифференциальная форма уравнения количества движения применительно к цилиндрической трубе при отсутствии трения имеет следующий вид:

.

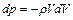Уравнение неразрывности в этом случае (dS = 0, dG = 0) дает

.

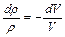Отсюда

.

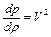Для политропического процесса 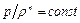при постоянном показателе политропы n, после дифференцирования имеем

,

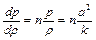так как скорость звука в газе .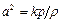

Приравнивая правые части последних выражений, замечаем, что показатель политропы в тепловом сопле является переменной величиной

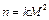. (2.65)

Формула (2.65) показывает наличие двух характерных сечений в тепловом сопле:

× в сечении, где 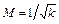местное значение показателя политропы равно единице (n = 1), т. е. элементарный термодинамический процесс в этом сечении – изотермический (dT = 0), и, следовательно, температура газа здесь проходит через максимум;

× в критическом сечении теплового сопла, т.е. при М = 1, показатель политропы на основании формулы (2.65) равен показателю идеальной адиабаты: 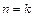, т. е. здесь имеет место элементарный изоэнтропический процесс, при котором, как уже указывалось выше, количество подведенной к газу теплоты и температура торможения проходят через максимум (, ).

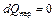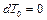На участке между изотермическим и критическим сечениями теплового сопла наблюдается понижение температуры газа (dT < 0) при подводе теплоты (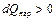). На этом участке сопла прирост кинетической энергии газа больше прироста энтальпии.

Для отыскания зависимости давления газа от числа М в тепловом сопле без трения воспользуемся уравнением количества движения в следующей форме:

.

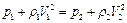отсюда

,

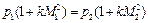или

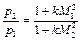. (2.66)

Иначе говоря, давление газа в тепловом сопле с ростом числа М монотонно падает, несмотря на увеличение полного давления в сверхзвуковой части.

Зависимость плотности газа и скорости течения в тепловом сопле от числа М можно найти следующим способом:

,

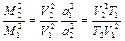но из уравнений состояния и неразрывности

,

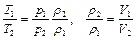поэтому

.

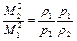Используя зависимость (2.66) получаем

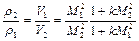, (2.67)

откуда видно, что плотность газа вдоль теплового сопла монотонно падает с ростом числа М.

Температура газа в тепловом сопле как функция числа М может быть получена делением равенства (2.66) на равенство (2.67):

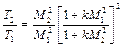. (2.68)

Кривая температуры имеет максимум в точке

.

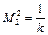В любых двух сечениях теплового сопла с одинаковой температурой (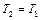) значения числа М, как это явствует из выражения (2.68), связаны следующей зависимостью:

.

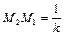При выводе формулы для параметров торможения в тепловом сопле число М в них заменим приведенной скоростью l, для чего можно воспользоваться известным соотношением, полученным ранее.

Температуру торможения найдем из равенства

.

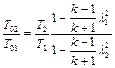Подставив в это выражение соотношение температур из (2.68) и заменив М на l, получим

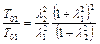. (2.69)

Полное давление в тепловом сопле может быть найдено из выражения

.

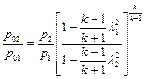Отсюда, используя равенство (2.66), приходим к следующей зависимости:

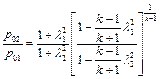. (2.70)

Плотность заторможенного газа в тепловом сопле можно определить путем деления выражения (2.70) на выражение (2.69):

.

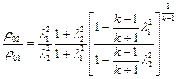Кривые изменения статического и полного давлений (рис. а), а также температур потока и торможения (рис. б) в тепловом сопле в зависимости от числа 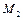при 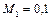приведены ниже.

Ошибка! Ошибка связи.

Ошибка! Ошибка связи.

Определим количество теплоты (Q), которое нужно подвести в тепловом сопле, чтобы изменить скорость газа от какого-либо одного значения (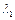) до другого (). При постоянной теплоемкости имеем:

,

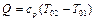или в безразмерном виде

.

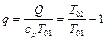Подставляя сюда отношение температур торможения из равенства (2.69), находим

.

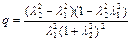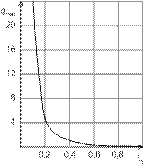Максимальное количество теплоты, отвечающее критическому подогреву (до 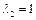), равно

.

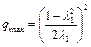Оно резко уменьшается с ростом начальной скорости газа (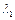) о чем свидетельствует график, приведенный на рисунке справа.

Предельно возможная скорость истечения из теплового сопла (при 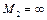) согласно равенству (2.68) зависит от начального значения числа M ₁.

.

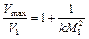В частности, если вести отсчет от критического сечения, т.е. положить 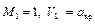, то получим

.

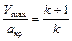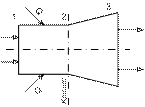Помимо четырех описанных «чистых» схем сверхзвуковых сопел, принципиально возможны комбинированные схемы. Наиболее реальным комбинированным соплом является так называемое полутепловое сопло, в котором дозвуковой участок является тепловым, а сверхзвуковой – геометрическим (см. рис. справа). В таком сопле газ ускоряется от некоторого начального дозвукового значения скорости до критического в цилиндрической трубе 1–2 за счет подвода теплоты, а переход к сверхзвуковой скорости и дальнейшее ускорение потока осуществляются без теплообмена в расширяющейся трубе 2–3. Расчет дозвукового участка полутеплового сопла ведется по формулам теплового сопла, а сверхзвукового участка – по формулам геометрического сопла.

Сравним полутепловое сопло с геометрическим при одинаковом конечном значении энтальпии (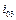) имея в виду, что в полутепловом сопле подогрев газа совершается в цилиндрической трубе 1–2, а в геометрическом сопле то же количество теплоты подводится к газу до его входа в сопло. Значения скорости истечения из обоих сопел одинаковы, так как в критических сечениях величина температуры торможения одна и та же. Полное давление на выходе из полутеплового сопла ниже в связи с наличием теплового сопротивления в его дозвуковом участке, поэтому ниже и статическое давление на выходе из полутеплового сопла.

Рассмотрим пример полутеплового сопла с начальной скоростью газа, соответствующей значению приведенной скорости 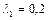. При этом безразмерная величина подогрева газа в дозвуковом участке сопла должна быть равна

.

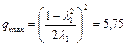Потери полного давления в полутепловом сопле (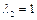) можно вычислить по формуле (2.70)

.

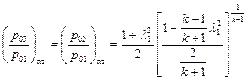При 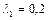и k = 1,4 имеем

.

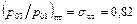Полное давление в геометрическом сопле сохраняет постоянное значение:

.

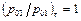Поэтому статическое давление на выходе из полутеплового сопла при одной и той же скорости истечения в 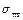раз отличается от статического давления на выходе из геометрического сопла:

.

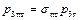Далее

,

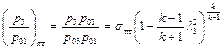где 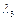– приведенная скорость истечения из сопла, р ₀₁ – полное давление в начальном сечении сопла.

При равных перепадах давления

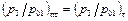
скорость истечения из полутеплового сопла меньше, чем из геометрического сопла (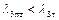).Это следует из равенства

,

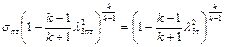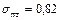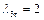связывающего отношение статического давления и полного с приведенной скоростью. Например, при и приведенная скорость истечения из полутеплового сопла 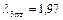, т.е. на 1,5% меньше приведенной скорости истечения из геометрического сопла.

Рассматривая различные типы сопел, предназначаемые для перехода через скорость звука, мы во всех случаях имели в виду переход от дозвуковой к сверхзвуковой скорости. Полученные формулы принципиально пригодны и для обратного случая, т.е. плавного преобразования сверхзвукового потока в дозвуковой. Однако при торможении сверхзвукового потока могут возникнуть скачки уплотнения, которые усложняют исследуемое явление.

Остановимся теперь кратко на совместном проявлении двух или нескольких воздействий. В качестве первого примера разберем случай геометрического сопла с трением. Основное соотношение (2.64) имеет в этом случае вид

.

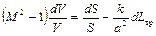Наиболее интересной особенностью этого сопла является то, что критическая скорость получается в его расходящейся части, так как при М = 1

,

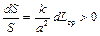а в узком сечени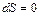и ( при 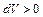) имеет место дозвуковая скорость и М < 1.

Выясним теперь главные особенности геометрического сопла с теплообменом. Из основного соотношения (2.64) в этом случае имеем

.

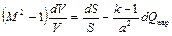Местоположение критического сечения (М = 1) определяется равенством

.

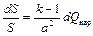При подводе теплоты (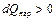) – например, при догорании газов в сопле – критическая скорость достигается в расходящейся части сопла (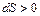). При отводе теплоты (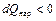), т. е. при теплоотдаче через стенки сопла, критическая скорость достигается в сужающейся части сопла (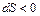). В первом случае в узком сечении сопла (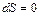) имеет место дозвуковая, а во втором случае – сверхзвуковая скорость.

Таким же путем можно исследовать совместное влияние в газовом течении любых других воздействий. При этом важно подчеркнуть, что в соответствии с уравнением (2.64) переход от М < 1 к М > 1 требует в любом случае изменения знака суммарного воздействия.

6 Расчет газовых течений с помощью газодинамических функций , ,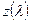

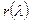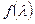
Рассмотрим газодинамические функции, которые используются в уравнениях количества движения газа. Сумму секундного количества движения и силы давления газа в рассматриваемом поперечном сечении потока принято называть полным импульсом потока I.

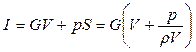(2.71)

Если в (2.71) подставить соотношения

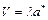и ,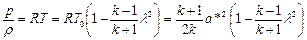

то получим

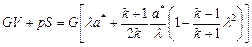. (2.72)

После раскрытия скобок и упрощений приводим выражение (2.72) к виду

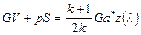, (2.73)

где .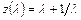

График газодинамической функции 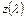для воздуха приведен ниже.

Минимальное значение функции 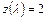соответствует критической скорости течения (). Как в дозвуковых, так и в сверхзвуковых потоках 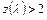. Значениям 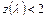не соответствуют какие-либо реальные режимы течения. При замене величины 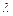обратной ей величиной 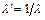значение функции 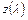не изменяется. Таким образом, од 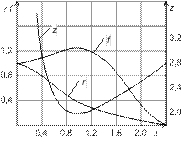ному значению 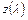могут соответствовать два взаимообратных значения приведенной скорости 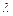– одно из них определяет дозвуковое, а другое – сверхзвуковое течение газа. Функция 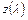не зависит от k.

Выражение (2.73) для импульса потока значительно упрощает запись и преобразования уравнения количества движения газа. Оно оказывается чрезвычайно полезным при решении широкого круга задач газовой динамики. Например, при расчете течений с ударными волнами, подводом теплоты и охлаждением, течений с трением, с ударом при внезапном расширении канала, при расчете процесса смешения потоков, при определении сил, действующих на стенки канала, при вычислении реактивной тяги и многих других.

Пример. Определить соотношения между параметрами газа до и после прямого скачка уплотнения.

Связь между параметрами газа в скачке уплотнения устанавливается из того, что при переходе через скачок сохраняются неизменными полная энергия, расход и импульс потока. Запишем те же уравнения с использованием газодинамических функций.

Уравнение количества движения или импульса потока

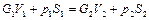
с учетом выражения (2.73) примет вид

.

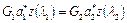Из уравнения сохранения расхода и полной энергии имеем

; ; .

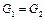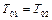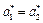Учитывая это, получим

.

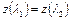Это уравнение имеет два решения: либо 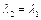, что соответствует безударному течению с неизменными параметрами газа, либо 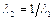, что соответствует прямому скачку.

По известному значению 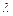с помощью уравнения неразрывности определяем изменение полного и статического давления в скачке уплотнения. Так как 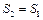и 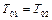, то используя формулы газодинамической функции 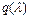, можно уравнение неразрывности для потока газа до и после скачка представить в виде

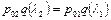
или

.

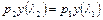Отсюда, учитывая, что 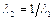, получаем

.

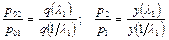Пример. Газ, движущийся в цилиндрической трубе, подогревается от 400 К на входе в трубу до 800 К на выходе из нее. Приведенная скорость потока на входе в трубу 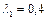. Требуется определить, пренебрегая трением, приведенную скорость потока после подогрева, а также изменение полного и статического давления в потоке.

Основное соотношение, определяющее закономерности течения газа в цилиндрической трубе с подводом теплоты, получим из уравнения количества движения

,

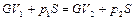так как подвод теплоты не связан с силовым воздействием на поток и силы давления в начальном и конечном сечении являются единственными силами, вызывающими изменение количества движения газа. Заменив выражения для импульса потока газа согласно соотношению (2.73) и считая, что теплоемкость газа и k при подогреве не изменяются, получим

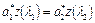или .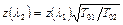

Так как при 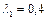, , 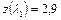то

.

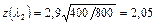С помощью таблиц функций 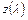или непосредственным вычислением из квадратного уравнения 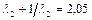определяем два возможных значения приведенной скорости на выходе: 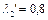, 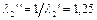. Реальным будет только первое решение, поскольку подогревом невозможно перевести дозвуковой поток в сверхзвуковой.

Зная 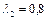, найдем 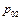и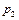

.

.

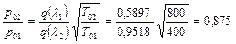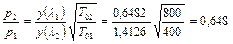Таким образом, как полное, так и статическое давление в результате подогрева газа уменьшаются. Полученное значение 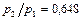и есть то соотношение давлений газа в начальном и конечном сечениях рассматриваемого участка трубы, которое необходимо создать, чтобы поддержать заданные температуры и приведенную скорость на входе .

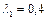Уравнение сохранения количества движения позволяет установить некоторые общие закономерности течения в цилиндрической трубе с подогревом или охлаждением. Видно, что с увеличением отношения 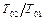величина функци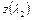й (при 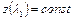) всегда уменьшается. Это означает, что с ростом подогрева в дозвуковом потоке 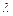увеличивается, а в сверхзвуковом – уменьшается. В обоих случаях скорость потока будет приближаться к критической (следовательно 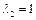, а 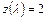). Это условие ограничивает величину предельно возможного подогрева для заданной начальной скорости потока .

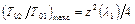Для принятых в данном примере значений параметров предельная величина подогрева соответствует .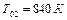

Из уравнений расхода можно определить отношение давлений 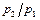, необходимое для реализации такого режима при сохранении 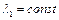. При увеличении подогрева сверх найденного значения получим 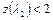, что указывает на физическую невозможность такого подогрева при заданной скорости течения на входе.

Заменив в соотношении (2.73) произведение 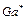его значением согласно (2.19) и (2.20), получим выражение для импульса газового потока в первом случае через полное давление, а во втором случае через статическое давление:

;

.

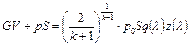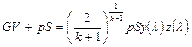Введем обозначения для двух новых функций приведенной скорости 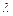, входящих в правые части этих выражений:

;

.

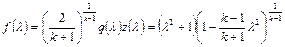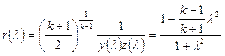Подставляя эти обозначения, получаем окончательно

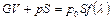; (2.74)

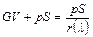. (2.75)

Функция 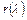введена, как величина, обратная произведению 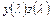с тем, чтобы облегчить пользование таблицами (произведение 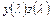быстро возрастает с увеличением 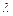, стремясь к бесконечности при 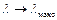. Величина же 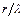изменяется в пределах от единицы до нуля). Графики функци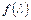й и 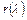приведены ранее.

Уравнения (2.74), (2.75) показывают ряд свойств импульса газового потока. В правой части этих уравнений отсутствуют величины расхода газа и температуры или критической скорости. Из этого следует, что если при заданной площади сечения S и приведенной скорости 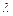полное или статическое давление в потоке постоянно, то импульс сохраняет постоянное значение независимо от температуры и расхода газа.

Физический смысл этого состоит в том, что при изменении температуры (или температуры торможения) газа при 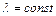скорость течения изменяется прямо пропорционально, а расход – обратно пропорционально корню квадратному из температуры, так что произведение GV остается постоянным. Отметим, что функция 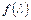в области дозвуковых и небольших сверхзвуковых скоростей изменяется очень мало (приблизительно на 10% в интервале ).

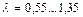Отсюда согласно (2.74) следует, что импульс газового потока при постоянных полном давлении и площади сечения слабо зависит от величины 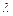в широком диапазоне ее изменения и определяется в основном величиной произведения .

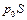Выражения (2.74) и (2.75) для импульса газа очень удобны при решении задач, связанных с определением сил, действующих со стороны газа на стенки канала, что необходимо, в частности, при вычислении реактивной тяги различных двигательных установок.