Задания для самостоятельной работы
Определить тип уравнения и привести к каноническому виду
1. 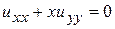 . 2.
. 2. 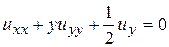 . 3.
. 3. 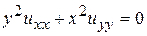 .
.
4. 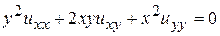 . 5.
. 5. 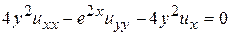 .
.
6. 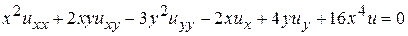 .
.
7. 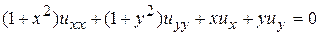 .
.
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Уравнение колебаний струны
Рассмотрим струну, под которой понимается тонкая нить, не сопротивляющаяся изгибу, длиной l. Пусть эта струна в плоскости (x,u) совершает малые поперечные колебания около своего положения равновесия, совпадающего с осью Ох, то есть все точки струны движутся перпендикулярно оси Ох. Обозначим через u(x,t) отклонение от положения равновесия точки струны с абсциссой х в момент времени t. Так как струна не сопротивляется изгибу, то ее натяжение 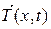 в точке х в момент времени t направлено по касательной к струне в точке х. Любой участок струны (а,b) после отклонения от положения равновесия в предположении о пренебрежении величинами высшего порядка малости по сравнению с
в точке х в момент времени t направлено по касательной к струне в точке х. Любой участок струны (а,b) после отклонения от положения равновесия в предположении о пренебрежении величинами высшего порядка малости по сравнению с 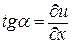 , не изменит своей длины
, не изменит своей длины
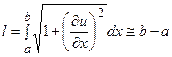 (16)
(16)
и, следовательно, величина натяжения 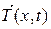 будет постоянной Т 0, не зависящей от х и t, так как закон Гука гласит: изменение натяжения пропорционально изменению длины выделенного участка.
будет постоянной Т 0, не зависящей от х и t, так как закон Гука гласит: изменение натяжения пропорционально изменению длины выделенного участка.
Составим уравнение движения струны. На элемент струны (х, 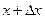 ) действуют силы натяжения
) действуют силы натяжения 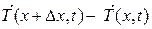 и внешняя сила
и внешняя сила 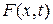 , действующая на струну в точке х в момент времени t и направленная перпендикулярно оси Ох.
, действующая на струну в точке х в момент времени t и направленная перпендикулярно оси Ох.
Сумма сил, действующих на струну, согласно закону Ньютона должна быть равна произведению массы элемента струны на его ускорение
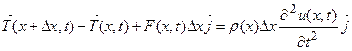 , (17)
, (17)
где 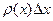 - масса элемента струны (х,
- масса элемента струны (х, 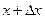 );
);
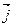 - единичный вектор, направленный вдоль оси u.
- единичный вектор, направленный вдоль оси u.
Проектируя векторное равенство (17) на ось u, получим
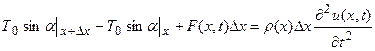 , (18)
, (18)
но в рамках приближения
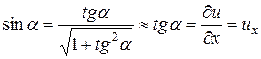 ,
,
поэтому выражение (18) принимает вид
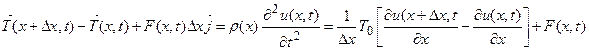
и при 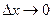 , получим
, получим
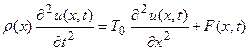 . (19)
. (19)
Это и есть уравнение малых поперечных колебаний струны. Если F(x,t)¹ 0, то колебания струны будут вынужденными, а если F(x,t)= 0, то колебания струны будут свободными.
Если 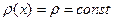 , то уравнение (19) принимает вид
, то уравнение (19) принимает вид
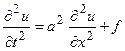 , (20)
, (20)
где 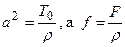 .
.
Уравнение (20) называется одномерным волновым уравнением. Для волнового уравнения может быть поставлена задача Коши, и в этом случае необходимо найти функцию u(x,t), удовлетворяющую начальным условиям
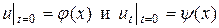
где 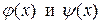 - заданные функции.
- заданные функции.
 2015-01-30
2015-01-30 762
762







