Кривые второго порядка

Кривая второго порядка – геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида

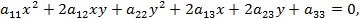
в котором, по крайней мере, один из коэффициентов 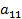, , 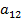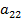отличен от нуля. Общее уравнение кривой можно записать в матричном виде

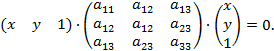
Невырожденная кривая второго порядка при

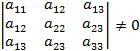
оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли квадратичная форма

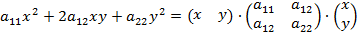
положительно определённой, отрицательно определённой, неопределённой или полуопределённой, что устанавливается по корням характеристического уравнения:

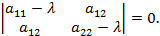
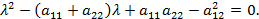
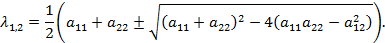
Вводом новой системы координат 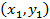можно привести уравнения кривых второго порядка к стандартному каноническому виду. Для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид окружности, эллипса, гиперболы или параболы.

1. Если собственные значения 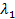и 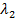одного знака, то уравнение кривой второго порядка можно привести к уравнению эллиптического типа:

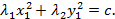
Есл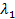и и 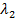имеют тот же знак, что и 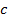, то имеем каноническое уравнение эллипса:

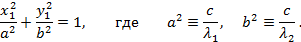
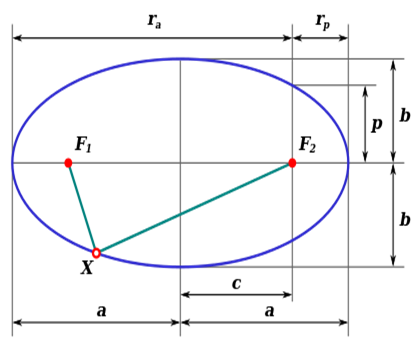
Эллипс – геометрическое место точек 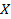плоскости, для которых сумма расстояний до двух данных точек 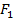и 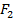, называемых фокусами, постоянна и больше расстояния между фокусам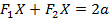и: при .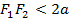

Если 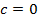, то уравнение 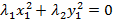имеет единственное решение при 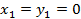, определяющее точку на плоскости.

Есл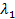и и 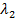имеют знак, противоположный знаку 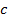, то имеем пустое множество решений, иногда называемое мнимым эллипсом:

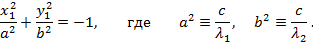
2. Если собственные значения 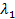и 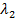разных знаков, то уравнение кривой второго порядка можно привести к уравнению гиперболического типа:

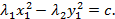
При 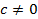оно сводится к одному из двух уравнений

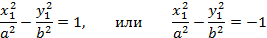
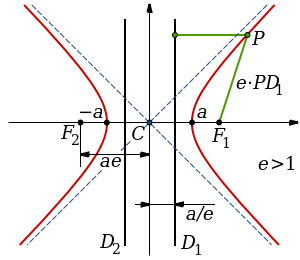
в зависимости от знака 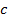. Оба этих уравнения определяют гиперболу – геометрическое место точек 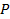плоскости, для которых абсолютное значение разности расстояний от точки 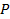до двух выделенных точек 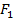и 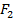, называемых фокусами, постоянно: 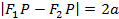при .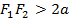

При 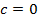получаем уравнение

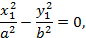
эквивалентное двум линейным уравнениям:

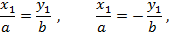
задающим пару пересекающих прямых.

3. Если одно из собственных значени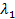й или 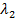равно нулю, то уравнение кривой второго порядка можно привести к уравнению параболического типа, которое можно привести к одному из следующих видов:

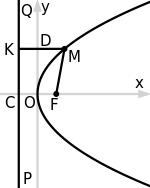
Уравнение 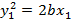определяет параболу – геометрическое место точек 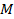, равноудаленных от данной прямой 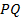, называемой директрисой, и данной точки 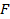, называемой фокусом параболы: .

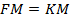Уравнение 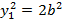, или 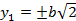определяет пару параллельных прямых.

Уравнение 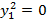определяет пару совпадающих прямых.

Уравнение 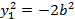не имеет решений, следовательно, не определяет никакого геометрического образа.

Пример. Записать в каноническом виде уравнение эллипса, проходящего через точки:

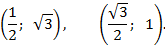
Решение: Каноническое уравнение эллипса, координатные оси которого совпадают с осями эллипса, имеет вид:

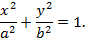
Значения осей эллипса 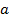и 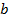найдем из двух условий:

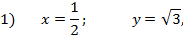
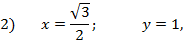
известных по условию задачи. Подставим эти значения в каноническое уравнение эллипса. Получим систему двух уравнений:

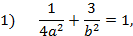
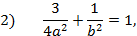
Разрешив систему этих двух уравнений относительно неизвестных 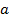и 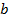, например, методом исключения, получим 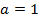, 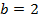. Таким образом, каноническое уравнение эллипса имеет вид:

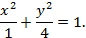
Ответ: Каноническое уравнение эллипса, проходящего через точки:

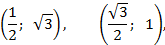
имеет вид:

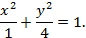
Пример. Уравнение гиперболы

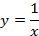
привести к каноническому виду.

Решение: В уравнении гиперболы 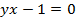сделаем замену переменных:

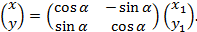
Тогда

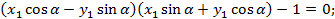
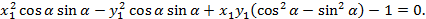
Поскольку каноническое уравнение гиперболы

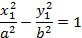
не содержит произведение 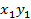, из условия 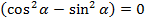следует, что 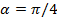. Подставляя значение 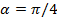в уравнение

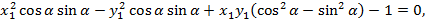
получим

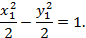
Ответ: Уравнение гиперболы

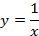
имеет канонический вид:

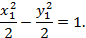
Пример. Определить вид кривой, определяемой уравнением

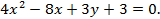
Вычислить основные параметры этой кривой.

Решение. Преобразуем исходное уравнение.

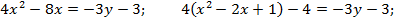
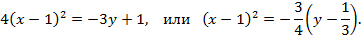
Последнее уравнение является каноническим уравнением параболы 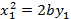с вершиной в точке

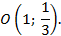
Ветви параболы направлены вниз.

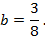
Фокус имеет координаты:

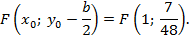
Директриса:

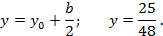
Ответ: Кривая, определяемая уравнением 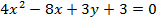, является параболой

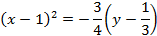
с ветвями, направленными вниз, с директрисой 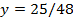, с фокусом в точке с координатами 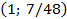, с вершиной в точке с координатами .

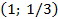Литература

1. Высшая математика для экономического бакалавриата. Учебник и практикум / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.
2. Кремер Н.Ш., Фридман М.Н. Линейная алгебра. Учебник и практикум / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.
3. Математика для экономистов и менеджеров. Учебник /под ред. Н.Ш. Кремера. – М.: Кнорус, 2014.
4. Математика для экономистов и менеджеров. Практикум /под ред. Н.Ш. Кремера. – М.: Кнорус, 2014.