Знакоопределенность квадратичной формы можно установить, исследуя главные миноры матрицы 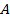 . Такой способ называется критерием Сильвестра:
. Такой способ называется критерием Сильвестра:
Действительная квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры ее матрицы положительны:
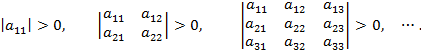
Действительная квадратичная форма является отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы чередуются, причем 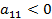 :
:
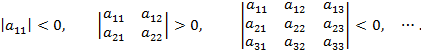
Пример. Методом Лагранжа найти нормальный вид и невырожденное преобразование, приводящее к этому виду, для следующей квадратичной формы.
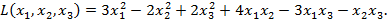
Решение: Метод Лагранжа заключается в выделении полных квадратов по всем переменным:
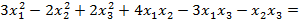
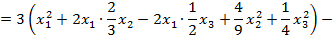
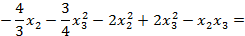
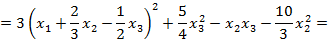
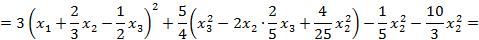
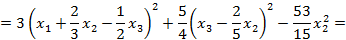
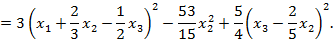
Пусть
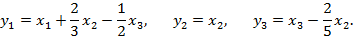
Тогда исходная квадратичная форма может быть приведена к каноническому виду:
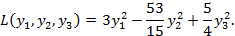
Сделав замену
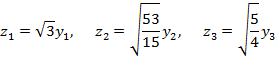
получим нормальный вид квадратичной формы
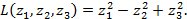
Ответ: Квадратичная форма
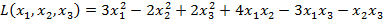
может быть приведена к нормальному виду
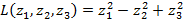
с помощью невырожденного преобразования
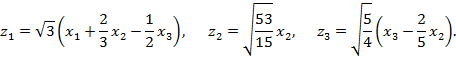
 2014-10-30
2014-10-30 12284
12284
