Степенной метод позволяет найти наибольшее по модулю собственное значение и собственный вектор.
Пусть 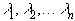 - собственные числа матрицы A. Для определенности предположим, что
- собственные числа матрицы A. Для определенности предположим, что
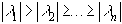
Берем произвольный ненулевой вектор  . Строим последовательность векторов
. Строим последовательность векторов
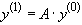 ,
, 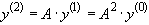 ,...,
,..., 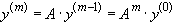
Тогда
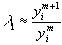 (38)
(38)
для любого номера i=1,2,...,n.
Точнее
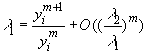 (*)
(*)
Докажем это в предположении, что матрица A имеет n линейных независимых собственных векторов 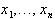 . Запишем разложение вектора
. Запишем разложение вектора  по базису из собственных векторов
по базису из собственных векторов
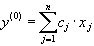 .
.
Тогда
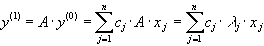
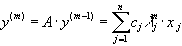
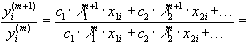
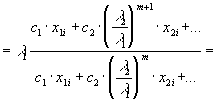

Так как 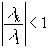 для k=2,...,n и
для k=2,...,n и 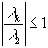 для k=3,...,n, то отсюда следует, что при
для k=3,...,n, то отсюда следует, что при 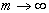 выполняется соотношение (*)
выполняется соотношение (*)
Взяв достаточно большой номер итерации m, мы сможем с любой степенью точности определить по формуле (38) наибольший по модулю корень 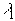 характеристического уравнения для матрицы A. Для нахождения этого корня может быть использована любая координата
характеристического уравнения для матрицы A. Для нахождения этого корня может быть использована любая координата 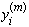 вектора
вектора 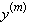 , в частности, можно взять среднее арифметическое соответствующих значений.
, в частности, можно взять среднее арифметическое соответствующих значений.
Так как 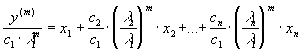 , то при
, то при 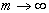
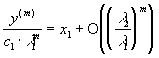 .
.
Поскольку собственный вектор определяется с точностью до скалярного множителя, то сам вектор 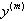 приближенно представляет собой собственный вектор матрицы A, соответствующий собственному значению
приближенно представляет собой собственный вектор матрицы A, соответствующий собственному значению 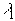 .
.
 2015-01-30
2015-01-30 2094
2094








