2015-01-30
259
Пусть существует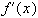 
, непрерывная на 
.
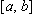По формуле Тейлора: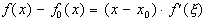 
.
Интегрируя, получаем:
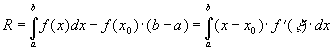(60)
Обозначим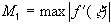 
.
Используем вариант теоремы о среднем, который имеет вид:
если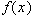 
непрерывна и 
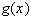- интегрируема, то 
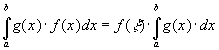, где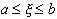 
.
Пусть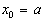 
. Имеем 
.
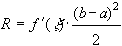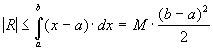(61)
Пусть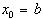 
. Имеем 
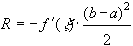и оценка для 
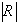будет того же вида (61).
Таким образом, (61) - оценка погрешности формул правых и левых прямоугольников.
Оценим погрешность для формулы средних прямоугольников.
Пусть существует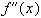 
. По формуле Тейлора имеем:
.
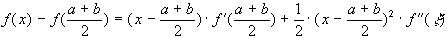Интегрируя, получаем
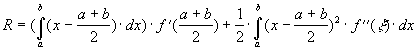
Так как,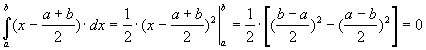 
, то
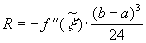. Отсюда следует оценка
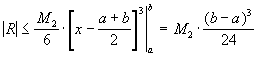(62)
Для повышения точности квадратурных формул можно промежуток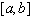 
разбить точками 
, 
, 
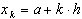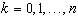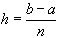на частичные промежутки, к каждому из которых применяется формула прямоугольников
, 
, 
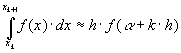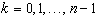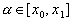(63)
Суммируя по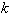 
, получаем обобщенную формулу прямоугольников.
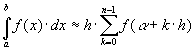(64)
при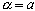 
- формула левых прямоугольников,
при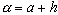 
- формула правых прямоугольников,
при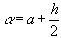 
- формула средних прямоугольников.
Оценка остаточного члена для обобщенной формулы получается на основе оценок (61) или (62) соответственно.
При , :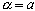
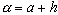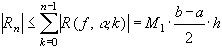(65)
При :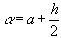 
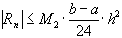
Из оценок (65) следует, что выбирая достаточно большое число точек разбиения (т.е. делая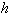 
достаточно малым) можно получить результат с необходимой точностью.
