2015-01-30
451
Однозначной задача определения параметров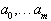 
станет, если рассматривать как показатель качества аппроксимации величину
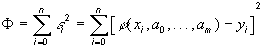(54)
и искать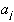 
, минимизирующие функцию 
.
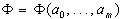Решение задачи о нахождении 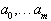в такой постановке называется методом наименьших квадратов.
В теории вероятностей показано, что полученные методом наименьших квадратов параметры наиболее вероятны, если отклонения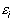 
подчиняются нормальному закону распределения. Необходимые условия минимума функции 
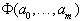дают систему уравнений
, 
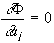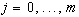(55)
Важный частный случай: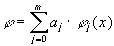 
, где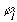 
- линейно независимые функции. Тогда система уравнений (55) будет линейной.
На практике часто используются функции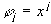 
. Тогда
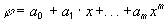- многочлен степени 
.
......................................................
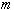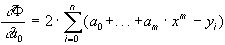
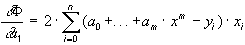
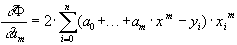
Таким образом, получается система следующего вида:
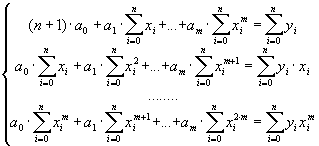(56)
При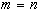 
полученный многочлен совпадает с интерполяционным многочленом Лагранжа.
[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]
[Home|Кафедра|ПетрГУ] 3.7. Квадратурные формулы.
Постановка задачи численного интегрирования.
Пусть требуется вычислить
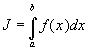(57)
Если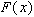 
- первообразная для 
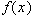, то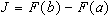 
. Часто получить выражение для первообразной не удается. Подинтегральная функция может быть задана в табличном виде. В этих случаях подинтегральную функцию заменяют на некоторую аппроксимирующую функцию, интеграл от которой легко вычисляется в элементарных функциях. Для аппроксимации подинтегральной функции часто используют интерполяцию. Во многих случаях формулы для приближенного вычисления интегралов (57) можно записать в виде
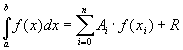(58)
Формулы такого вида называются квадратурными.
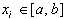- узлы квадратурной формулы.
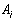- коэффициенты.
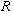- погрешность (остаточный член) квадратурной формулы.
