Нахождение решения неявной разностной схемы

20 21 22 23 24 25 26

Двухточечная неявная схема Адамса (19) имеет вид нелинейного уравнения относительно неизвестного значения :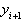

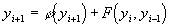, (20)

где

, .

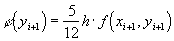Для решения уравнения (20) на каждом шаге можно предложить метод простых итераций:

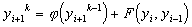. (21)

Решение уравнения получается как предел последовательности, состоящей из приближений 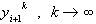. Достаточное условие сходимости метода простых итераций выглядит следующим образом:

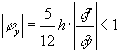Это условие выполняется для достаточно малого шага 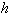(чем меньше 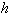, тем быстрее сходится метод). Кроме того для работы метода (21) необходимо получить из каких-то соображений начальное приближение .

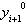4.9.4. Схема "предиктор - корректор". Сравнение методов

В качестве начального значения для итерационного процесса (21) можно использовать приближенное решение 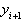, полученное с помощью явной схемы Адамса:

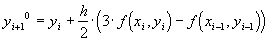
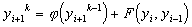Такое совместное использование экстраполяционной и интерполяционной разностных схем называется методом "предиктор - корректор" ("прогноз - коррекция"). Вопрос о количестве итераций 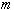, выполняемых на каждом шаге, решается по разному. Иногда итерации производят до тех пор, пока не выполнится условие

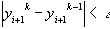
при заданной точности 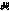. Чаще на каждом шаге выполняют фиксированное число итераций 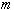, как правило, небольшое. Иногда .

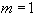Основываясь на формулах, приведенных в разделах 3.8.1 и 3.9.1, нетрудно выписать разностные схемы Адамса для 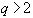. На практике используется метод "предикор - корректор", состоящий из явной четырехточечной и неявной трехточечной схем Адамса. Эти схемы имеют вид:

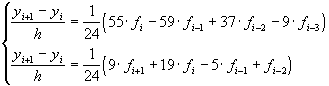
Подводя итог изучению одношаговых и многошаговых методов решения задачи Коши, отметим, что многошаговые (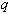 -шаговые) методы для начала счета требуют знания приближенных значений решения в 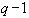точке (кроме уже заданных начальных условий), т.е. эти методы не являются само стартующими. Для вычисления значений в 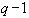точке используется вспомогательный одношаговый метод (например, Рунге - Кутта). Вспомогательный одношаговый метод также используется в том случае, когда требуется в процессе вычисления изменить шаг.

Преимуществом многошаговых методов является то, что при переходе к следующей точке требуется однократное вычисление правой части 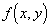дифференциального уравнения, а в методах Рунге - Кутта - многократное. Однако это преимущество можно использовать только в методах "предиктор - корректор", поскольку сравнение остаточных членов метода Рунге-Кутта 4-го порядка и явного метода Адамса 4-го порядка показывает, что коэффициент в остаточном члене метода Рунге-Кутта в 960 раз меньше коэффициента в остаточном члене метода Адамса, т.е. при одинаковой точности схема Рунге-Кутта позволяет брать шаг в 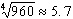раз больше, чем в схеме Адамса, а значит, фактически потребуется меньше вычислений правой части, чем в методе Адамса.