Рассмотрим линейное дифференциальное уравнение второго порядка в самосопряженной форме
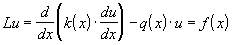 (28)
(28)
на интервале 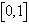 с краевыми условиями первого рода:
с краевыми условиями первого рода:
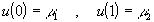 (29)
(29)
Если 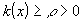 ,
, 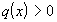 , то такая краевая задача описывает стационарное распределение тепла в стержне (- температура в точке
, то такая краевая задача описывает стационарное распределение тепла в стержне (- температура в точке 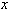 ,
, 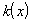 - коэффициент теплопроводности). Задача имеет единственное решение, если
- коэффициент теплопроводности). Задача имеет единственное решение, если 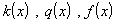 - кусочно-непрерывные функции. Возможны также другие типы краевых условий:
- кусочно-непрерывные функции. Возможны также другие типы краевых условий:
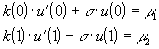 (30)
(30)
При 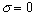 эти условия называются краевыми условиями второго рода, при
эти условия называются краевыми условиями второго рода, при 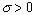 - условиями третьего рода.
- условиями третьего рода.
Введем на отрезке 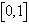 равномерную сетку
равномерную сетку

и запишем трехточечную разностную схему для краевой задачи (28)-(29) в прогоночном виде
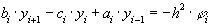 ,
, 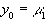 ,
, 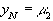 (31)
(31)
где коэффициенты 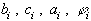 зависят от значений функций
зависят от значений функций 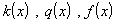 в узлах сетки, а также от шага
в узлах сетки, а также от шага 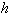 .
.
Перепишем разностную схему (31) в виде
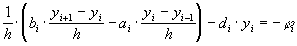 ,
, 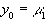 ,
, 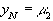 (32)
(32)
где 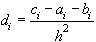 . Схема называется однородной, если ее коэффициенты во всех узлах сетки для любого линейного дифференциального уравнения вычисляются по одним и тем же правилам. Для однородной схемы удобна система безиндексных обозначений:
. Схема называется однородной, если ее коэффициенты во всех узлах сетки для любого линейного дифференциального уравнения вычисляются по одним и тем же правилам. Для однородной схемы удобна система безиндексных обозначений:
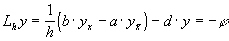 (33)
(33)
Здесь 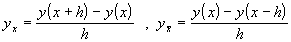 .
.
Найдем погрешность аппроксимации схемы (33):

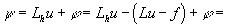
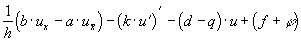
Пользуясь теперь разложением
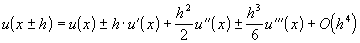
получаем:
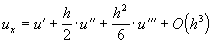 ,
, 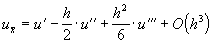
Тогда погрешность аппроксимации предстанет в виде:
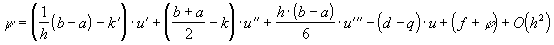
Таким образом, схема (33) будет иметь второй порядок аппроксимации, если будут выполнены условия:
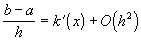 ,
, 

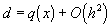 ,
, 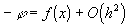
Например, эти условия выполняются при
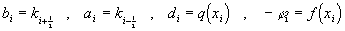 (34)
(34)
где 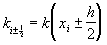 . Действительно,
. Действительно,
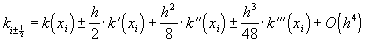 ,
,
поэтому
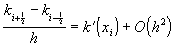 ,
, 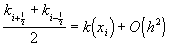 .
.
 2015-01-30
2015-01-30 890
890








