Сходимость разностной схемы

Для исследования сходимости рассмотрим погрешность разностной схемы в узлах сетки:

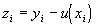
Пользуясь линейностью оператора (33) и введенными ранее безиндексными обозначениями, нетрудно установить, что погрешность в узлах сетки удовлетворяет разностной схеме

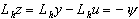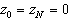, (35)

где - погрешность аппроксимации.

Выведем оценку для погрешности в узлах сетки 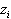. Из соотношений (34) следует, что

, ,

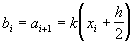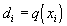поэтому схема (35) в прогоночном виде (31) запишется следующим образом:

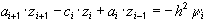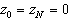, (36)

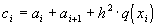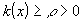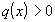
где . Предположим, что в исходном линейном дифференциальном уравнении (28) , 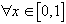. Тогда, в частности, имеет место неравенство:

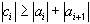(37)

Значения 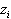из схемы (36) можно найти, используя так называемый метод прогонки. Попробуем переписать схему в виде

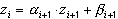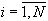, (38)

с неизвестными коэффициентами 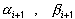. Подставив в формулу (36) соотношение 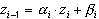, получим

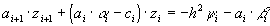
или

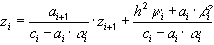
Таким образом, схема (36) разрешима в виде (38), если 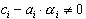. В этом случае для 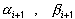получаем рекуррентные формулы:

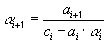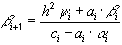, (39)

Для начального условия 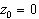уравнение (38) принимает вид

,

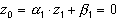откуда получаем начальные условия для уравнений (39): 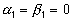. Теперь можно вычислить все значения 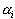, , 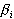, 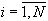а затем спуститься "вниз" по 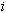от 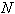до 1 и найти все значения 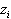по формуле (38).

Заметим, что если 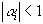, то

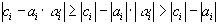
и тогда из неравенства (37) и формул (39) следует, что

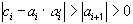и .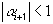

Поскольку известно, что 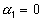, то по индукции мы получаем, во-первых, разрешимость схемы (36) в виде (38), и во-вторых, справедливость неравенства

.

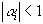
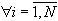Следовательно, из формулы (38) можно вывести неравенство:

.

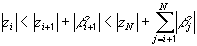Учитывая, что 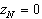, получаем соотношение: 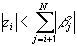. Воспользуемся теперь рекуррентной формулой (39) для 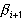, умножив ее на положительную величину :

.

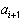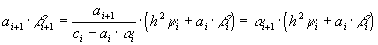Тогда 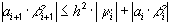, следовательно,

,

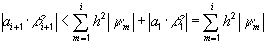учитывая, что 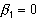. Наконец, поскольку 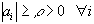, можно сделать вывод, что

.

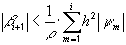Таким образом, для погрешности в узлах сетки 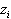можно записать неравенство

,

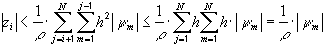
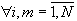потому что 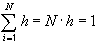. Переходя к нормам, получаем

,

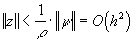то есть разностная схема (33) для краевой задачи (28)-(29) при условиях на коэффициенты (34) имеет второй порядок сходимости.