Часть 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 2.1.
Точечные оценки основных параметров распределения
| Оцениваемый параметр генеральной совокупности | Его выборочная точечная оценка | ||||||
По простой выборке
n - объём выборки |
По сгруппированным данным
| xi | x 1 | x 2 | … | xi | … | xl |
| mi | m 1 | m 2 | … | mi | … | ml |
mi – частота встречаемости значения признака xi; 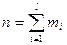 - объём выборки
- объём выборки
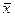
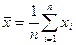 (2.1)
(2.1)
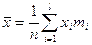 (2.2)
(2.2)
 (2.3)
(2.3)
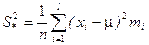 (2.4)
(2.4)
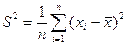 (2.5)
или
(2.5)
или 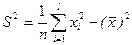 (2.7)
(2.7)
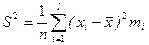 (2.6)
или
(2.6)
или 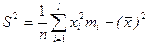 (2.8)
(2.8)
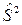
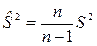 (2.9)
(2.9)
 (2.10)
(2.10)
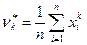 (2.11)
(2.11)
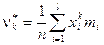 (2.12)
(2.12)
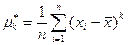 (2.13)
(2.13)
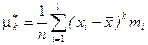 (2.14)
(2.14)
Очевидно, что средняя арифметическая равна выборочному первому начальному моменту  , а выборочная дисперсия – выборочному второму центральному моменту
, а выборочная дисперсия – выборочному второму центральному моменту 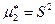 .
.
Связь между центральными и начальными моментами задается формулами:
μ 2* = ν 2* – (ν 1*)2
μ 3* = ν 3* – 3 ν 2* ν 1*– 2(ν 1*)3
μ 4* = ν 4* – 4 ν 3* ν 1*+ 6 ν 2* ν 1*– 3(ν 1*)4
Средняя арифметическая 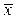 , вычисленная по n независимым наблюдениям над случайной величиной X, является состоятельной и несмещенной оценкой математического ожидания μ = MX:
, вычисленная по n независимым наблюдениям над случайной величиной X, является состоятельной и несмещенной оценкой математического ожидания μ = MX: 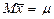 . Если случайная величина X распределена нормально с параметрами N (μ, σ), то оценка
. Если случайная величина X распределена нормально с параметрами N (μ, σ), то оценка 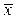 математического ожидания имеет минимальную дисперсию
математического ожидания имеет минимальную дисперсию 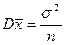 , т.е. является эффективной оценкой.
, т.е. является эффективной оценкой.
Оценка выборочной дисперсии 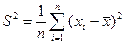 является смещенной. Если математическое ожидание неизвестно, то несмещенной оценкой дисперсии является исправленная выборочная дисперсия
является смещенной. Если математическое ожидание неизвестно, то несмещенной оценкой дисперсии является исправленная выборочная дисперсия 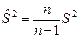 (2.9) (дробь
(2.9) (дробь 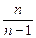 называют поправкой Бесселя).
называют поправкой Бесселя).
Таблица 2.2.
 2015-01-30
2015-01-30 632
632







