Методы штрафных функций

Идея метода штрафных функций состоит в следующем. Исходную задачу математического программирования

Min j (x) = m (1)
x є X

заменяют задачей о безусловной минимизации однопараметрической функции

M(x,b) = j (x) + (1/b)y (x),

либо задачей минимизации функции M(x,b) на некотором множестве Г, более простой структуры с точки зрения численных методов минимизации, чем исходное множество Х.
При этом функцию y (x) выбирают таким образом, чтобы решение задачи

min M(x, b) = m(b) (2)
x є Г

сходилось при b(r) 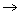0 к решению исходной задачи, или если это обеспечить не удается, то по крайней мере чтобы

m(b) 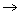m при b(r) 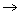0.

Итак, метод штрафных функций состоит в построении функции М(х, b), в выборе последовательности {b_i} и в решении соответствующих этой последовательности задач вида (2).
Имеются два главных, в основе своей различных, подхода к построению построению штрафных функций. Первый подход, известный как метод внешних штрафных функций, был предложен Курантом в 1943 г., когда почти все хорошо известные сейчас алгоритмы нелинейного программирования еще только разрабатывались. В методе внешних штрафных функций штрафы выбираются так, что точки вне С (замкнутое множество в пространстве Rⁿ) последовательно по мере возрастания и становятся все более "невыгодными" и либо m_i(b) = 0 для всех bєC, либо m_i(b) 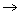0 при i (r)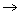 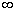для всех bє C.

Второй подход называется методом внутренних штрафных функций. В нем штрафные функции выбираются так, чтобы оптимальные для задач (2) точки b_i принадлежали внутренности С⁰ множества С. Благодаря этому свойству штрафных функций методы внутренних штрафных функций известны также как барьерные методы, поскольку в процессе решения задачи они "отталкивают" от границы множества С точки b. Поэтому начальная точка b⁰, используемая при решении задачи (2), должна выбираться из С⁰.
Основные свойства методов штрафных функций: при достаточно слабых предположениях они строят последовательности, сходящиеся к точкам, оптимальным для задачи (2) определяемой (1). В то же время все результаты опираются на значительную идеализацию ситуации, поскольку мы предполагаем, что можем решать задачи минимизации без ограничений (2). Возникает две проблемы. Первая из них состоит в решении вопроса о "начале и конце", или, точнее, о прерывании процесса построения минимизирующей последовательности {b_i}. Вторая проблема касается достоинств различных методов штрафных функций.

Пусть задано число e > 0 и мы хотим найти точку 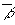. Все методы штрафных функций строят точки b_i, являющиеся оптимальными решениями для задачи (2).
Таким образом, в принципе, существует такое целое число j, что точка b_j удовлетворяет нашим требованиям. Предположим, что это целое число j, которое на практике оказывается очень большим, нам известно, и допустим, что мы хотим найти минимум функции f⁰(b) + m_j(b), исходя из некоторого начального приближения b⁰, с помощью одного из алгоритмов, требующего вычисления градиента. Весьма вероятно, что f⁰(b⁰) будет слишком мало по сравнению с m_j(b), если m_j - внешняя штрафная функция, или слишком велико, если m_j(b) - внутренняя штрафная функция.
Обычная практика состоит в том, чтобы начать со штрафа умеренной величины и затем увеличивать его в процессе вычислений. Существует много ситуаций, когда имеет смысл комбинировать методы внешних и внутренних штрафных функций и создавать смешанные методы.