2015-01-30
523
генерация кодовых последовательностей
и сигналов управления
В данной работе изучаются особенности Z-преобразования кодовых последовательностей и схем их генерации. Работа включает теоретический анализ, расчетную часть и компьютерный эксперимент по генерации различных вариантов кодовых последовательностей.
расчетное задание
Исходная кодовая последовательность (состоящая из нулей и единиц) задается рекуррентным уравнением:
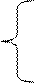1, n = 0,
Сn = a1 Сn-1 + a2 Сn-2 + Сn-3 , mod 2,
0, n ³ N.
Здесь полагается, что Сn = 0, n< 0; параметры a1 и a2 могут принимать только два значения – нуль или единицу; сложение – по модулю 2; граница последовательности задана условно.
Датчик подобной последовательности может служить примером имитатора источника сообщения или сигнала управления.
Из анализа следует, что такие последовательности имеют циклический характер. Период последовательности не превышает значения, см. (36),
Lmax = 2m – 1,
где m – порядок (глубина) связей. В данном случае m = 3 и Lmax = 7.
Расчетную часть выполните в следующем порядке.
1. Для анализа вариантов запишите значения, которые может принимать последовательность С0, С1, …, С7. Обратите внимание на закономерности:
С1 + С3 = 1, mod 2,
С2 + С7 = 0, mod 2,
С4 + С6 = 1, mod 2.
Они могут служить тестом для проверки на «четность» и «нечетность».
Определите условие (a1 =?, a2=?), при которых последовательность Сn имеет максимальный период: Сn = Сn+7, (Lmax = 7).
Составьте все варианты (по табл. 4), последовательностей С0, С1, …, С7,
проверьте указанные закономерности и запишите значения соответствующих периодов Li, i = 1, 2, 3, 4.
Таблица 4
| Вариант | a1 | a2 | Li |
2. Для первого варианта последовательности Сn
Сn = d(n) + Сn-3, mod 2
с условиями (режимами генерации)
а) Сn = 0, n ³ L1 (однократный режим),
б) Сn =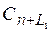 
(многократный режим)
необходимо:
- записать полные алгоритмы формирования;
- определить Z-преобразования D1(z);
- для контроля путем обращения Z-преобразования проверить значения С0 и С1;
- составить рекурсивные схемы генерации;
- проверить, возможна ли нерекурсивная схема генерации в режиме «а».
3. Для второго варианта последовательности Сn
Сn = d(n), + Сn –1 + Сn -2 + Сn -3, mod 2
с аналогичными условиями: а) Сn = 0, n ³ L2 и б) Сn =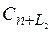 
– выполните те же процедуры, что и выше. При составлении нерекурсивного варианта схемы генерации в режиме «а» воспользуйтесь формулой (33).
4. Для третьего и четвертого вариантов последовательностей Сn
(М-последовательностей!)
Сn = d(n), + Сn –2 + Сn -3, mod 2,
Сn = d(n), + Сn –1 + Сn -3, mod 2,
с условиями генерации: а) Сn = 0, n ³ Lmax = 7, и б) Сn = Сn+7 – выполните все указанные выше действия. При анализе этих вариантов схем проверьте и убедитесь в следующем:
- двучлен 1 + Z-7 (для Lmax = 7) имеет три неприводимых множителя, и только два из них являются «порождающими» (порождают
М-последовательность);
- делением двучлена 1 + Z-7 на «порождающий» многочлен можно получить «проверочный» многочлен – он и является системной функцией нерекурсивного варианта схемы генерации.
5. Составьте общую рекурсивную схему генерации (см. пример – рис. 11) последовательности Сn, предусмотрев в нерекурсивной части элемент сдвига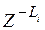 
(для каждого варианта) и параметр b в двух режимах генерации:
а) b = 1 (однократная генерация);
б) b = 0 (многократная генерация).
Запишите в общем виде алгоритм функционирования схемы.
Для всех ситуаций представьте графики последовательностей Сn.
лабораторное задание
Работа выполняется на компьютере в среде Matlab. Ознакомьтесь с краткой инструкцией, (см. прил. 2). Обратите внимание на особенности модульной арифметики.
1. В среде Matlab составьте рекурсивные схемы и алгоритмы генерации последовательности в первом варианте (см. табл.4) с режимами работы «а» и «б». Результаты выведите на экран и оформите графиком. Проверьте расчетные предпосылки.
2. Повторите процедуру компьютерного моделирования для второго варианта параметров. Результаты выведите на экран и оформите графиком. Проверьте расчетные предпосылки.
3. Составьте рекурсивную схему генерации М-последовательности (с третьим вариантом параметров a1 и a2 ). Предусмотрите два режима запуска «а» и «б». Запустив схему, выведите результаты на экран. Для контроля проверьте работу схемы по алгоритму ее функционирования. Составьте нерекурсивный вариант схемы генерации с периодическим запуском. Результаты генерации выведите на экран и оформите графиками.
4. Повторите весь процесс моделирования для четвертого варианта параметров a1 и a2. Проверьте расчетные предпосылки. Результаты оформите графиками.
5. Составьте общую рекурсивную схему генерации последовательности Сn. Устанавливая соответствующие значения параметров (Li, b, a1, a2), выполните контрольные проверки работы схемы.
содержание отчета
Отчет по работе должен включать расчетную часть и компьютерный эксперимент в соответствии с пунктами заданий:
a. исходные модели последовательностей Сn;
b. их Z-преобразования и анализ (разложение на множители);
c. контрольные и тестовые проверки;
d. схемы и алгоритмы генерации;
e. результаты моделирования (графики и пояснения)
f. выводы по работе.
контрольные вопросы
i. Какие особенности аппарата Z-преобразований следует иметь в виду в применении к бинарным (кодовым) последовательностям и схемам их генерации? Поясните на примерах.
ii. Приведите полный вывод системной функции (39) для генератора последовательности Cn конечной длины.
iii. Покажите, что последний полином в записи (40) не может порождать М-последовательность с L = 15 элементами.
iv. Определите системные функции генераторов М-последовательностей (42) и (43) в нерекурсивном варианте. Проверьте результаты генерации.
v. Предложите схемы периодического запуска нерекурсивных схем генерации последовательностей Сn. Возможен ли здесь режим периодического запуска со сменой знака?
vi. Какие элементы схемы генерации М-последовательности обеспечивают ее обнуление при однократном режиме работы?
vii. Укажите причины, по которым произвольная рекурсивная схема генерации последовательности (состоящая из нулей и единиц) обязательно имеет периодичность.
