Эффекты квантования в схемах генерации

дискретных сигналов

В данной работе изучаются эффекты, к которым приводят ограничения на точность представления параметров ЛПП-систем, используемых для генерации сигналов. Работа включает теоретический анализ, расчетную часть и компьютерный эксперимент по моделированию генераторов с усеченными значениями параметров.

расчетное задание

Для исследования эффектов квантования в работе используются две разновидности дискретных сигналов:

e^-ak , k = 0 (1) N₀–1,

U(k) =

0 k < 0, k ³ N₀;

cos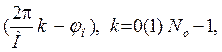

V(k) =

0, k < 0, k ³ N₀.

При подготовке к компьютерному эксперименту предварительно необходимо составить идеализированные и имитационные (с учетом усечения параметров) схемы и алгоритмы генерации указанных сигналов, выполнить контрольные проверки и произвести оценки ожидаемых погрешностей.

При составлении идеализированных схем и алгоритмов генерации используйте результаты лаб. работы №1.

В имитационных моделях схем генерации сигналов U(k) и V(k) необходимо учесть следующие особенности.

Схема генерации сигнала U(k) содержит параметры, значения которых меньше единицы (a = e <1, α > 0). В данном случае используйте процедуру усечения дробных чисел по нижеприведенной схеме.

Здесь E₁(•) – односторонний квантователь, n – число сохраняемых разрядов после десятичной запятой. Эту схему включают только в рекурсивную часть генератора. В нерекурсивные части схем усеченные значения параметров вносятся непосредственно (см. рис. 22,б и 23,б).

Чтобы отличить процессы генерации в нерекурсивных и рекурсивных схемах, в первом случае используйте обозначение U_ус(k), во втором – U_кв(k). Таким образом будет отмечено наличие квантователя в схеме генерации.

Предусмотрите два режима усечения: n = 1 и n = 2. (Шаг квантования и число уровней квантования соответственно равны: ∆x=∆a=10 , К_max=10ⁿ –1).

В схеме генерации сигнала V(k) (см. рис. 6) усечению подлежат только три параметра: b₀, b₁ и a₁. Они могут иметь положительные и отрицательные значения и превышать единицу (см. a₁). Процедуру их усечения выполните с учетом масштабного множителя по нижеприведенной схеме.

10

Здесь E₂(•) – двусторонний квантователь, n – число сохраняемых разрядов (один – в целой части и n-1 – в дробной части). Эту схему внесите только в звено с параметром a₁. В нерекурсивную часть схемы усеченные значения параметров b₀ и b₁ вносятся непосредственно.

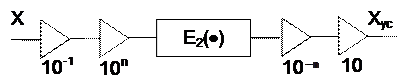Предусмотрите два режима усечения: n=2 (сохраняется один разряд после запятой) и n=3 (сохраняется два разряда после запятой).

Расчетную часть выполните в приведенной ниже последовательности.

1. Для модели U(k), N₀=5 c параметром a = e^–α (значение α задается по варианту α = 0,1; 0,2; 0,3; 0,4):

- составьте идеализированные схемы и алгоритмы генерации (в двух вариантах);

- представьте имитационные модели этих схем и соответствующие алгоритмы;

- вычислите значения отсчетов сигнала U(k), k=0(1)N₀-1, по исходному выражению и занесите их в табл. 2;

- вычислите значения отсчетов сигнала U_ус(k), k=0(1)N₀-1, по алгоритму нерекурсивной схемы генерации для двух режимов усечения и занесите их в табл. 2;

- вычислите последовательно значения отсчетов U_кв(0), U_кв(1), … по алгоритму рекурсивной схемы генерации для двух режимов усечения и занесите их в табл. 2, обратите внимание на значения U_кв(k) на тактах k≥N₀=5;

- по данным табл. 2 вычислите ожидаемые погрешности ξ² и η² при генерации сигнала по нерекурсивной и рекурсивной схемам для двух режимов усечения

,

.

Таблица 2

К
U(k)
Uус(k)	n=1
n=2
Uкв(k)	n=1
n=2

2. Для модели V(k), N₀=M=8 с параметром φ₀ (значение φ₀ задается по варианту φ₀=0; π/6; π/3; π/2):

- составьте идеализированную и имитационную схемы и алгоритмы генерации в рекурсивном варианте;

- вычислите значения отсчетов V(k), k=0(1)N₀-1 по исходному выражению и занесите их в табл. 3;

- вычислите последовательно значения отсчетов V_кв(0), V_кв(1), … по алгоритму работы имитационной схемы для двух режимов усечения и занесите их в табл. 3, обратите внимание на значения отсчета V_кв(N₀);

- по данным табл. 3 вычислите ожидаемую погрешность при генерации сигнала для двух режимов усечения

.

Таблица 3

K
V(k)
Vкв(k)	n=2
n=3

лабораторное задание

Работа выполняется на компьютере в среде MatLab. Ознакомьтесь с краткой инструкцией и демонстрационными примерами (см. прил. 2).

Пункты лабораторного задания выполняются в соответствии с пунктами предварительной подготовки.

1. В среде MatLab (приложение Simulink) составьте нерекурсивную схему генерации сигнала U(k), внесите усеченные значения параметров (два режима усечения: n=1, n=2). Запустите схему единичным отсчетом. Результаты выведите на экран, сравните с данными табл. 2.

Повторите эксперименты с рекурсивным вариантом схем для тех же режимов усечения. Обратите внимание на значения отсчетов генерируемого сигнала U_кв(k) на тактах k=N₀, N₀+1, …

Пункт заканчивается сравнительным анализом расчета и эксперимента, построением графиков сигналов U(k) и U_кв(k).

2. В среде MatLab составьте имитационную модель схемы генерации сигнала V_кв(k) в двух режимах усечения: n=2, n=3. Запустите модель единичным отсчетом. Результаты выведите на экран, сравните с данными табл. 3. Обратите внимание на значения отсчетов V_кв(k) на тактах k= N₀, N₀+1, …. Пункт заканчивается сравнительным анализом расчета и эксперимента, построением графиков сигналов V(k) и V_кв(k).