Пусть объект исследования может находиться в некоторых состояниях, число которых конечно (равно n). Номера состояний 0,1,2,…n. Из i-го состояния в j- е объект переходит с постоянной интенсивностью λi j, обратно – с постоянной интенсивностью μji.
Применение дифференциальных уравнений, для определения вероятностей состояний объекта, рассмотрим на примере объекта, изображенного на рисунке 3.4




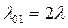
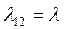


 |  | ||||||
 | |||||||
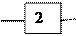 | |||||||
а)
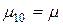
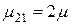
б) Граф состояний
Рис. 3.4
Число состояний три. Состояние S0 – два элемента (1 и 2) – работоспособны. S1 – один из элементов (1 или 2) – в отказовом состоянии, S2 – оба элемента в отказовом состоянии.
По виду графа состояния можно составить систему дифференциальных уравнений Колмогорова по следующему правилу.
Для каждого из возможных состояний объекта записывается уравнение, в левой части которого dPi/dt, а справа – столько слагаемых, сколько стрелок графа соприкасается с данным состоянием. Если стрелка направлена в данное состояние, то перед слагаемым ставиться плюс, если стрелка направлена из данного состояния - минус. Каждое из слагаемых будет равно произведению интенсивности перехода из данного состояния (либо в данное состояние) на вероятность состояния из которого выходит стрелка
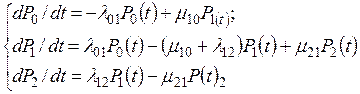
Можно упростить уравнение, если учесть, что рассматриваемый процесс – процесс марковский стационарный, т.е. можно принять, что dPi(t)/dt = 0
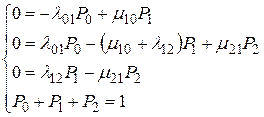
Четвертое уравнение при трех неизвестных необходимо, т.к. первые три уравнения сводятся к двум. Решение системы уравнений даст:
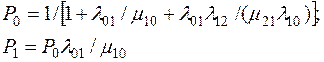
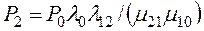 .
.
Результаты решения системы можно получить непосредственно по виду графа состояний, если пользоваться следующим правилом: вероятность нулевого состояния определяется выражением:
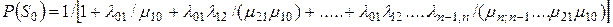 ,
,
где числитель правой части – всегда единица; знаменатель - сумма, состоящая из единицы и дробей, числители которых – произведения интенсивностей на верхних стрелках, знаменатели – произведения интенсивностей на нижних стрелках (произведения формируются с последовательным увеличением числа множителей от одного до n в соответствии с переходами 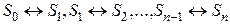 ).
).
Вероятность состояния 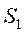 равна вероятности состояния
равна вероятности состояния 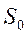 , умноженной на коэффициент равный второму слагаемому в знаменателе для
, умноженной на коэффициент равный второму слагаемому в знаменателе для 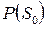 , т.е.
, т.е. 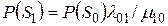
Вероятность состояния 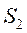 равна вероятности состояния
равна вероятности состояния 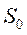 умноженной на коэффициент, равный третьему слагаемому в знаменателе для
умноженной на коэффициент, равный третьему слагаемому в знаменателе для 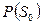 , т.е.
, т.е. 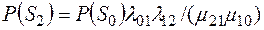
Вероятность n- го состояния равна вероятности состоянии 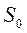 , умноженной на коэффициент равный последнему (n -му), слагаемому в знаменателе для
, умноженной на коэффициент равный последнему (n -му), слагаемому в знаменателе для 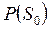 , т.е.
, т.е.

Пример: Определить вероятность состояний объекта, схема которого и граф состояний изображены на рис 3.4, если интенсивности отказов λ0 элементов 1 и 2 равны 0,02, а интенсивности восстановления 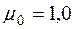
Интенсивности переходов объекта в состояние S0, S1, S2 равны:
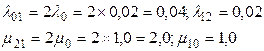
Вероятность состояния S0
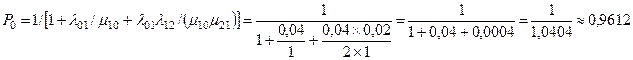
Вероятность состояния S1
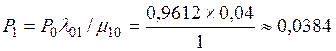
Вероятность состояния 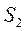
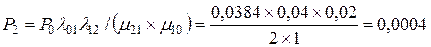
 2015-01-30
2015-01-30 570
570








