Косвенные измерения

При косвенных измерениях измеряемая величина А является функцией от 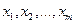, т.е. 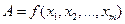. Для простоты считают, что значения 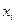распределены по нормальному закону, измерения равноточные, погрешности измерения 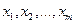не коррелированы (если погрешность не вызвана каким-либо общим фактором, изменяющимся случайным образом, например, температурой).

Очевидно, что абсолютные погрешности измеряемой величины 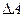являются функцией погрешности прямых измерений:

.

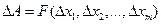В простейшем случае для одной переменной 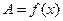в результате измерений получим

.

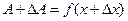Разложим правую часть в ряд Тейлора и сохраним члены разложения, содержащие 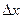в первой степени:

.

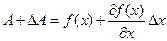Отсюда абсолютная 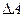и относительная 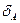погрешности

.

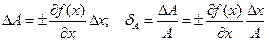В общем случае для функции 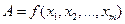абсолютную погрешность результата косвенных измерений определяют как сумму случайных погрешностей:

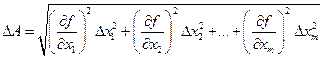. (4.4)

Относительная погрешность

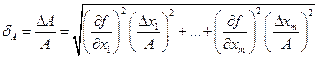. (4.5)

Если число опытов при измерении каждой из величин 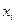принять равным n, то измеряемая величина 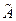- функция средних арифметических :

.

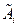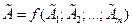В формулы (4.4), (4.5) вместо 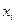подставляют .

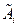В табл. 4.2 приведены оценки абсолютных и относительных погрешностей измерений для наиболее часто встречающихся функций.

Т а б л и ц а 4.2. Оценки абсолютных и относительных погрешностей при косвенных измерениях

Функция вида	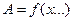Погрешности
Абсолютная	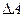Относительная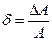
Сх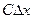

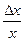
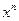
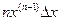
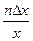
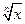
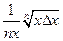
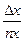
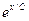
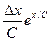
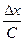
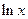
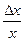
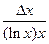
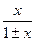
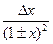
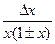
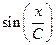
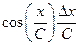
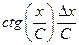
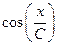
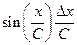
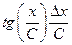
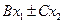
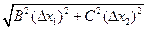
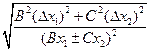
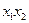
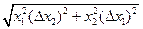
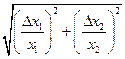
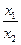
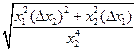
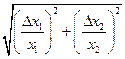
Примечание. С, В – постоянные величины.