1. Внешнее представление:
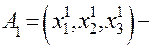 первая точка на оси вращения поверхности;
первая точка на оси вращения поверхности;
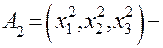 вторая точка на оси вращения поверхности;
вторая точка на оси вращения поверхности;
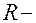 радиус цилиндрической поверхности.
радиус цилиндрической поверхности.
В собственной системе координат 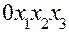 уравнение цилиндрической поверхности имеет вид:
уравнение цилиндрической поверхности имеет вид:
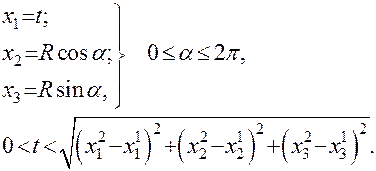 (7.4)
(7.4)
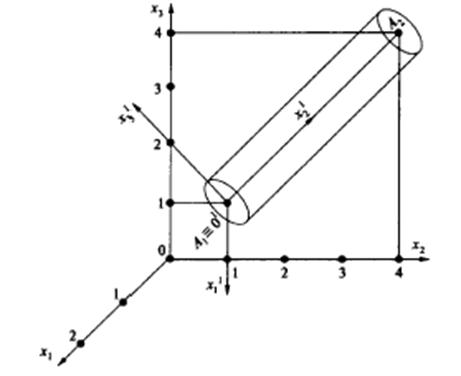
Рисунок 7.2
Матрица преобразований 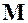 координат получается с использованием последовательных движений: параллельного переноса системы на вектор
координат получается с использованием последовательных движений: параллельного переноса системы на вектор 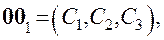 и последовательных вращений абсолютной системы координат вокруг осей Ох1 и Ох2 на углы α, β соответственно.
и последовательных вращений абсолютной системы координат вокруг осей Ох1 и Ох2 на углы α, β соответственно.
Рассмотрим частный, конкретный случай:
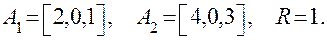
Уравнение цилиндрической поверхности в собственной системе координат имеет вид
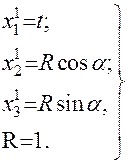 .
.
Матрица преобразования координат будет иметь вид
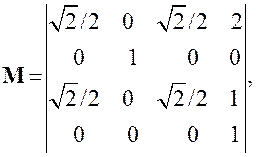
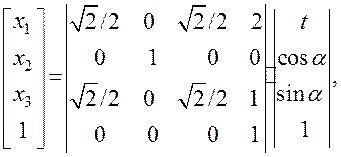 (7.5)
(7.5)
где
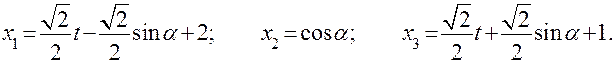
Окончательно, уравнение цилиндрической поверхности
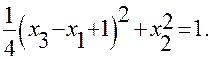
 2015-01-30
2015-01-30 695
695








