При автоматизированном проектировании технологических процессов изготовления детали возникает необходимость выявления их геометрических свойств на основе описания К основным свойствам относятся: объем детали, площади ограничивающих поверхностей, их протяженность в различных направлениях, возможность обработки поверхностей при заданной схеме базирования и обработки с данного направления и др.
Необходимым элементом всех алгоритмов выявления геометрических свойств является предикат Р(А) принадлежности точки А рассматриваемой детали D. С помощью предиката можно рассматривать деталь D путем сканирования точки А на достаточно плотной сетке области расположения детали и выявлять необходимые ее свойства.
Рассмотрим сущность предиката Р(А) и его использование при распознавании требуемых свойств детали.
Пусть задана деталь D – плоский квадрат со стороной 1 (рисунок 6.1, описание – (6.2), (6.3)). Деталь изображена на рисунке 7.7.
Символом G обозначен габаритный параллелепипед, определяемый неравенствами:
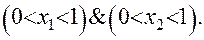
Предикат Р(А) определяется как булева функция, аргументом которой является точка 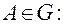
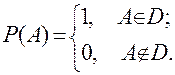
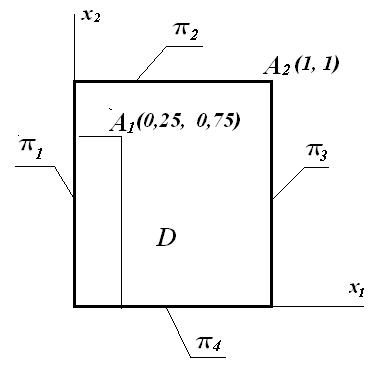
Рисунок 7.7
Иными словами, функция Р(А) принимает значение 1 (истинна), если точка А принадлежит детали D.
Алгоритм вычисления функции Р(А) содержит два этапа:
- вычисление булева вектора 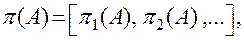 где
где 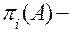
булева функция одного переменного А, определяющая условие попадания точки А в полупространство,
- образованное поверхностью 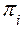 ; п – количество поверхностей
; п – количество поверхностей 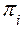 ,
,
ограничивающих деталь D;
- вычисление значения булевой функции 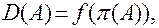 определяющая
определяющая
логические условия относительного расположения полупространств,
образованных плоскостями 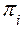 .
.
Покажем на примере процедуру вычисления предиката Р(А) для точек 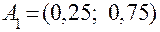 и
и 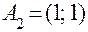 (рисунок 6.7).
(рисунок 6.7).
Векторы 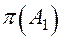 и
и 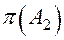 , определяющие условия расположения точек
, определяющие условия расположения точек 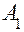 и
и 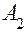 относительно полупространств, ограниченных поверхностями
относительно полупространств, ограниченных поверхностями 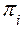 , имеют вид:
, имеют вид:
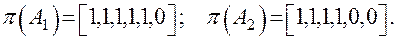
Функция 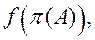 определяющая уравнение детали, имеет вид:
определяющая уравнение детали, имеет вид:
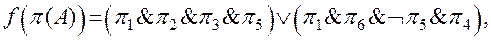
то есть точка 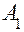 принадлежит
принадлежит 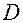 , а точка
, а точка 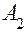 не принадлежит
не принадлежит 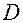 .
.
 2015-01-30
2015-01-30 581
581








