2015-01-30
1131
Внешнее представление
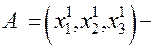координаты центра большой окружности;
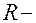радиус большой окружности;
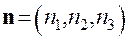-- вектор нормали к плоскости центров малых окружностей;
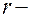радиус малой окружности.
Уравнение поверхности в собственной системе в двухпараметрической форме
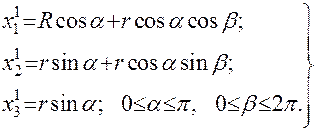(7.9)
Матрица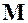 
преобразований получается за счет последовательности движений:
- параллельного переноса начала координат на величину вектора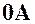 
;
- последовательных вращений абсолютной системы координат вокруг осей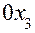 
и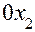 
на углы 
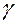и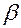 
.
Матрица 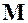преобразований координат вычисляется так же как и для цилиндрической поверхности. Рассчитаем уравнение тороидальной поверхности, используя матрицу преобразований
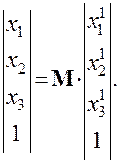(7.10)
Вычисляем обратную матрицу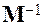 
и подставляем координаты
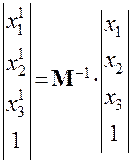(7.11)
в соотношения (7.9), далее вычисляем полученные уравнения относительно параметров и находим окончательно уравнение тороидальной поверхности в абсолютной системе координат.
