Прочитайте предложенные рассуждения и примеры. Ответьте письменно на вопросы и решите задачи.
Напомним для начала, что числовая последовательность – это бесконечный упорядоченный набор чисел. Члены последовательности можно пронумеровать, так что каждому натуральному значению n (1,2,3,…) соответствует член последовательности (а 1, а 2, а 3,…). Таким образом, последовательность – это функция, заданная на множестве натуральных чисел. Задают последовательность чаще всего формулой общего члена. Например, если 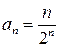 , то первые члены этой последовательности:
, то первые члены этой последовательности:
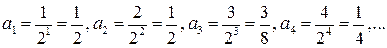
Понятие предела последовательности поясним пока на простых примерах:
- Последовательность натуральных чисел 1,2,3,4,5,… неограниченно возрастает или стремится к плюс бесконечности: n ®+¥. Поскольку n – натуральные числа и не могут быть отрицательными, знак «+» обычно опускают, подразумевая его «по умолчанию», и пишут n ®¥.
- Последовательность 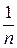 :
: 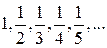 стремится к 0 при n ®¥. Действительно, при очень больших значениях n значения
стремится к 0 при n ®¥. Действительно, при очень больших значениях n значения 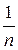 становятся очень
становятся очень
маленькими, так что, хотя члены этой последовательности не становятся равны 0, но отграничить их от 0 невозможно: начиная с некоторого номера все члены этой последовательности оказываются ближе к 0, чем любое заранее выбранное число e. Это легко понять, например если изобразить члены последовательности точками на числовой прямой.
Пишут: 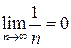 (предел при n ®¥ равен 0) или иногда
(предел при n ®¥ равен 0) или иногда 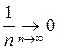 .
.
- Сходным образом 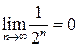 и т.п. Вообще, если числитель дроби постоянен, а знаменатель неограниченно взрастает, то вся дробь стремится к 0.
и т.п. Вообще, если числитель дроби постоянен, а знаменатель неограниченно взрастает, то вся дробь стремится к 0.
При вычислении пределов последовательностей пользуются простыми их свойствами:
- предел суммы равен сумме пределов (если последние существуют и конечны);
- предел произведения равен произведению пределов (если последние существуют и конечны);
- предел отношения равен отношению пределов (если последние существуют и конечны и предел знаменателя не равен 0).
Примеры.
1. Вычислить 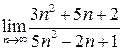 .
.
Решение: При n®¥ и числитель и знаменатель дроби стремятся к бесконечности. Говорят, что имеет место неопределенность вида 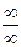 .
.
Из трех слагаемых числителя быстрее всего возрастает слагаемое старшей степени, т.е. 3n2. Вынесем за скобки n2:
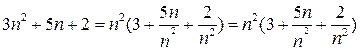
Аналогичным образом преобразуем знаменатель:
 .
.
В целом получаем:
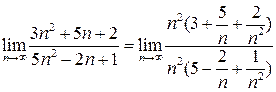
Заметим, что слагаемые 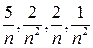 при n®¥ стремятся к 0 и, таким образом, после сокращения дроби на n2, имеем:
при n®¥ стремятся к 0 и, таким образом, после сокращения дроби на n2, имеем:
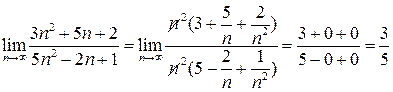 .
.
2. Вычислить 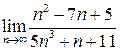 .
.
Решение: Имеется неопределенность вида 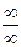 . Преобразуем дробь, вынеся за скобки старшую степень n в числителе и знаменателе:
. Преобразуем дробь, вынеся за скобки старшую степень n в числителе и знаменателе:
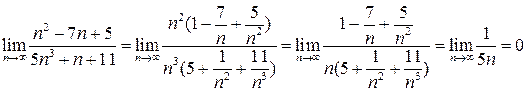 .
.
3. Вычислить 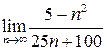 .
.
Решение: Имеется неопределенность вида 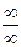 . Преобразуем дробь:
. Преобразуем дробь:
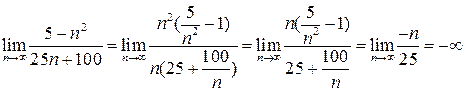
4. Вычислить 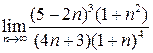 .
.
Решение: Имеется неопределенность вида 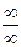 . Преобразуем дробь, вынеся старшую степень из каждого множителя:
. Преобразуем дробь, вынеся старшую степень из каждого множителя:
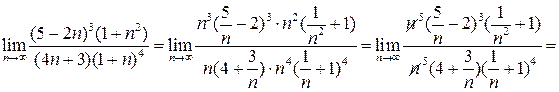
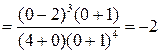
 2015-01-30
2015-01-30 418
418








