Ранг матрицы равен наибольшему порядку отличного от нуляминору.
На этой теореме базируется еще один метод нахождения ранга матрицы - метод окаймления миноров. Суть этого метода заключается в нахождении миноров, начиная с низших порядков и двигаясь к более высоким. Если минор 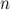 -го порядка не равен нулю, а все миноры
-го порядка не равен нулю, а все миноры 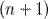 -го равны нулю, то ранг матрицы будет равен
-го равны нулю, то ранг матрицы будет равен 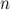 .
.
Пример
Задание. Найти ранг матрицы 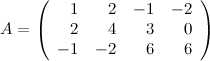 , используя метод окаймления миноров.
, используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы 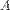 . Рассмотрим, например, минор
. Рассмотрим, например, минор 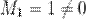 . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
. расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор 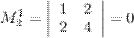 ; рассмотрим еще один минор второго порядка, для этого минор
; рассмотрим еще один минор второго порядка, для этого минор 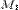 окаймляем при помощи второй строки и третьего столбца, тогда имеем минор
окаймляем при помощи второй строки и третьего столбца, тогда имеем минор 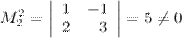 , то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
, то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор 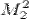 . Таких миноров два: комбинация третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
. Таких миноров два: комбинация третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
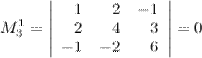
так как содержит два пропорциональных столбца (первый и второй); второй минор
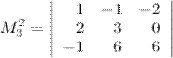
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
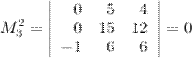
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы 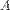 равен двум:
равен двум: 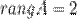
Ответ. 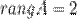
 2015-01-30
2015-01-30 402
402








