Предел числовой последовательности: определение, свойства

Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, число 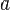называется пределом последовательности 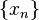, если для любого 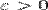существует номер 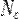, зависящий от 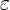такой, что для любого 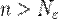выполняется неравенство .

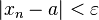Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.

Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые ирациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.

В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.

Определение

Число 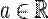называется пределом числовой последовательности 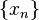, если последовательность 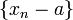является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

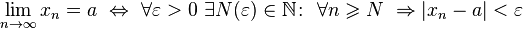
В случае, если у числовой последовательности существует предел в виде вещественного числа 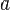, её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

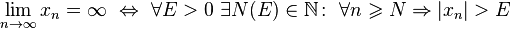
Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

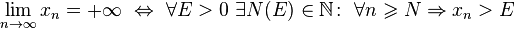
Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

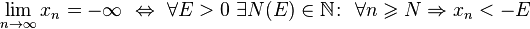
Частичный предел последовательности — это предел одной из её подпоследовательностей.

Верхний предел последовательности — это наибольшая из её предельных точек.

Нижний предел последовательности — это наименьшая из её предельных точек.

Существуют определённые особенности для предела последовательностей вещественных чисел.

Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств.

Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела.