Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых естьинтегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Определённый интеграл как площадь фигуры
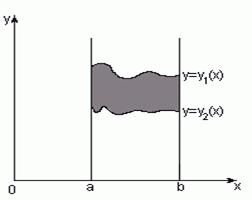
Определённый интеграл 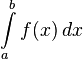 численно равен площади фигуры, ограниченной осью абсцисс, прямыми
численно равен площади фигуры, ограниченной осью абсцисс, прямыми 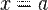 и
и 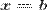 и графиком функции
и графиком функции 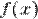 .
.
Формула Ньютона — Лейбница
Основная статья: Формула Ньютона — Лейбница
11.Свойства определенного интеграла.
Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.
Теорема 1. Если f (x) и g (x) - две непрерывные функции, заданные на промежутке [ a, b ], то
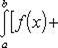
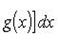
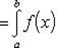
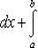
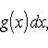
т. е. интеграл суммы равен сумме интегралов слагаемых.
В самом деле, составляя интегральную сумму для функции f (x) + g (x), очевидно, будем иметь
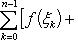
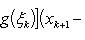
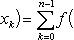
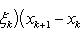
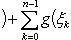
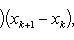
после чего остается перейти к пределу при λ → 0.
Аналогично доказывается
Теорема 2. Если f (x) - непрерывная функция, а c - постоянное число, то
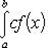
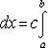
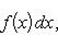
т. е. постоянный множитель можно выносить за знак интеграла.
Теорема 3. Пусть f (x) непрерывна на промежутке [ a, b ]. Если этот промежуток точкой c разложен на части [ a, c ] и [ c, b ], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
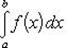
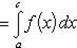
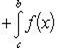
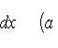
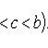
В самом деле, будем при раздроблении промежутка [ a, b ] на части включать c в число точек деления. Если c = xm, то
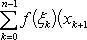
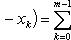
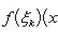
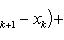
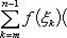
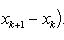
Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [ a, b ], [ a, c ] и [ c, b ]. Остается перейти к пределу при λ → 0.
Если 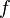 непрерывна на отрезке
непрерывна на отрезке 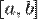 и
и 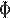 — её любая первообразная на этом отрезке, то имеет место равенство
— её любая первообразная на этом отрезке, то имеет место равенство
Приложения определенного интеграла.
Приложения определенного интеграла.
1. Вычисление площади криволинейной трапеции.
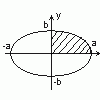 Пример. Вычислить площадь ограниченную эллипсом
Пример. Вычислить площадь ограниченную эллипсом 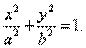
Ввиду очевидной симметрии эллипса относительно осей координат, достаточно вычислить четвёртую часть площади, расположенную в правом верхнем квадранте.
Из уравнения эллипса находим y как функцию от x: y(x)=b 
Тогда площадь эллипса вычисляем по формуле:
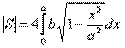 Сделав замену x=a sin t,
Сделав замену x=a sin t, 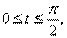 получим интеграл:
получим интеграл: 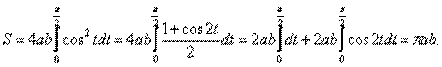
2. Вычисление объёмов тела, площади сечения которых известны.
|
|

Пусть для некоторого тела в пространстве известно значение S(x) – площади сечения этого тела плоскостью, проходящей через точку x’ и параллельной плоскости OYZ.
Тогда объём этого тела может быть вычислен по формуле 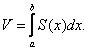
Пример. Вычислить объём эллипсоида 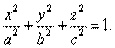
В сечении эллипсоида плоскостью, проходящей через точку x, 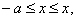 параллельной плоскостью OYZ будет эллипс:
параллельной плоскостью OYZ будет эллипс: 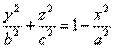 или
или 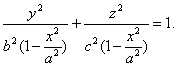
Как было доказано в предыдущем примере, площадь S(x) этого эллипса равна 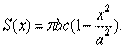
Следовательно, объём эллипсоида можно вычислить по формуле:
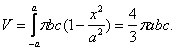
3. Вычисление длинны дуги плоской кривой.
Пусть кривая Г задана на плоскости OXY уравнением y=y(x), 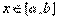 и
и 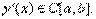
Тогда длинна этой кривой может быть вычислена по формуле:
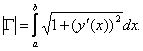
Пример. Вычислить длину окружности x2 + y2 = R2.
В силу симметрии окружности относительно осей координат, достаточно длину четверти окружности, лежащей в первом квадранте. Выражая из уравнения окружности y как функцию от x: 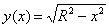 и подставляя значение
и подставляя значение 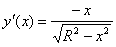 в формулу для вычисления длинны дуги кривой, получим равенство:
в формулу для вычисления длинны дуги кривой, получим равенство:
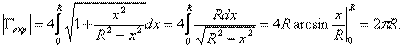
4. Вычисление площади поверхностей вращения плоской кривой вокруг неподвижной оси.
Пусть кривая Г, заданная как и выше уравнением y=y(x), 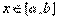 ,
, 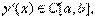 вращается вокруг оси OX. Тогда площадь поверхности вращения этой кривой может быть вычислена по формуле:
вращается вокруг оси OX. Тогда площадь поверхности вращения этой кривой может быть вычислена по формуле:
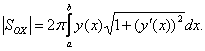
Пример. Вычислить площадь поверхности сферы x2 + y2 + z2 = R2.
Площадь поверхности сферы можно представить как площадь поверхности вращения кривой 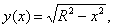
 вокруг оси OX.
вокруг оси OX.
Пользуясь формулой для площади поверхности вращения кривой вокруг оси OX, получим значение площади поверхности сферы:
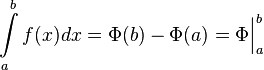
 2015-01-30
2015-01-30 1251
1251








