Метод деления пополам

Найти W(x) на отрезке [a,b].

Шаг 1. x_m=(a+b)/2; L=b-a; вычислить W(x_m).

Шаг 2. x₁=a+L/4; x₂=b-L/4; вычислить W(x₁) и W(x₂).

Шаг 3.

· Если W(x₁)<W(x_m), то исключить (x_m,b], т.е. b=x_m, x_m=x₁. Перейти к шагу 5.

• Если W(x₁) 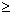W(x_m), то перейти к шагу 4.

Шаг 4.

· Если W(x₂)<W(x_m), то исключить [a,x_m), т.е. a=x_m, x_m=x₂. Перейти к шагу 5.

• Если W(x₂) 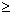W(x_m), то исключить [a,x₁) и (x₂,b], т.е. a=x₁, b=x₂. Перейти к шагу 5.

Шаг 5. L=b-a. Если | L| <e, то закончить поиск. В противном случае вернуться к шагу 2.

Продолжение примера 2.1. Оптимальный раскрой лесоматериалов (MathCAD) (рис.2.1)

Как видно из алгоритма, из каждых трех значений целевой функции W, вычисленных в интервале поиска, в дальнейшем используется только два, а третья не дает дополнительной информации и в дальнейшем не используется.

Программа:

Рисунок 2.1 - Решение примера 1.

Метод золотого сечения

Сущность метода. Интервал поиска делится на две части так, чтобы отношение длины большого отрезка к длине всего интервала было равно отношению

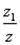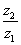= . Учитывая, что z1+z2=z, имеем	W(x)	z
z12=z z2 = (z1+z2)z2 = z1z2 + z22;		z1	z2
z1z2 + z22 - z12 = 0,
откуда 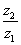= 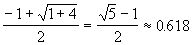.	а	x	b	x

Рисунок 2.2. Определение коэффициента дробления

Найти W(x) на отрезке [a, b].

Шаг 1. Вычисляем коэффициент дробления отрезка [a, b] k=(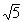 - 1)/2.

Шаг 2. x₁=a+(1-k)(b-a), вычислить W(x₁).

Шаг 3. x₂=a+k(b-a), вычислить W(x₂).

Шаг 4.

· Если | x₂-x₁| < , где  - заданная погрешность, то x^m = (x₁+x₂)/2, вычислить W(x^m) и закончить поиск.

• Если | x₂-x₁| >, то перейти к шагу 5.

Шаг 5.

· Если W(x₁)>W(x₂), то исключить a=x₁, x₁=x₂ и W(x₁)=W(x₂). Перейти к шагу 3, затем к шагу 4.

• Если W(x₁) <W(x₂), то b=x₂, x₂=x₁ и W(x₁)=W(x₂). Перейти к шагу 2 и 4.

Таким образом, применение методов исключения интервалов накладывает единственное ограничение на исследуемую целевую функцию - унимодальность. Следовательно, рассмотренные методы можно использовать для анализа как непрерывных, так и разрывных и дискретных функций. Логическая структура поиска основана на простом сравнении значений функции в двух пробных точках.

Метод золотого сечения

В методе золотого сечения целевая функция вычисляется в точках интервала, расположенных таким образом, чтобы каждое вычисленное значение целевой функции давало бы новую полезную информацию.

Необходимо найти минимум функции f = x⁴-14x³+60x²-70x. Проведем вычисления методом золотого сечения на интервале (1;2) с погрешностью 1e-5.
Программа будет иметь вид:

Примечание program prim; uses crt, ustp, metodo, idvvod; {*------Подключение модулей ------* UstP - Установка параметров и типов, открытие файла для работы MetodO - Методы нахождения оптимума функции 1- переменной без ограничений IDVvod - Процедуры ввода исходных данных для методов оптимизации } var a,b,e:real; nom:integer; fil:text; {$F+} {- обязательно подключать директиву!!! } {--Описываем функцию, оптимум которой необходимо найти--} function q(x:real):real; begin q:=x*x*x*x-14*x*x*x+60*x*x-70*x; end; {---Основная программа ---} Begin Clrscr; {--Выводим строку для удобства пользователя, т.е. уточняем метод--} writeln('Нахождение оптимума по методу "золотого" сечения'); {--Подключаем процедуру получения имени файла для ввода результатов --} GetInputName(fil); {--Подключаем процедуру ввода исходных данных --} VvodIsx_GS(a,b,e,fil); {--Подключаем процедуру вычисления оптимума --} GoldSech(q,a,b,e,fil); {--Закрываем файл результатов--} close(fil); end.