Минимизировать W(x)=2x2+(16/x) в интервале 1 < x < 5.
W'(x) = dW(x)/dx = 4x-16/x2.
Итерация 1.
Шаг 1. N=1, P=5, W'(5)=19.36, W'(1) = -12.
Шаг 2. R=5-{19.36/[(19.36+12)/4]}=2.53.
Шаг 3. W'(2.53)=7.62>0; положить R=2.53.
Итерация 2.
Шаг 2. R=2.53-{7.62/[(7.62+12)/1.53]}=1.94.
Шаг 3. W'(1.94)=3.51>0; положить R=1.94.
Итерации продолжаются до тех пор, пока не будет выполняться неравенство | W'(R)| < .

Метод касательных
Сущность метода. Ориентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны. Работа алгоритма начинается из точки xo, которая представляет начальное приближение корня уравнения W'(x)=0. Далее строится линейная аппроксимация функции W'(x) в точке x1, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. Если точка xk принята в качестве текущего приближения к оптимальной точке, то линейная функция, аппроксимирующая функцию W'(x) в точке xk, записывается в виде
W'(x,xk) = W'(xk) + W''(xk)(x-xk).
Приравняв правую часть уравнения к нулю, получим следующее приближение к искомой точке.
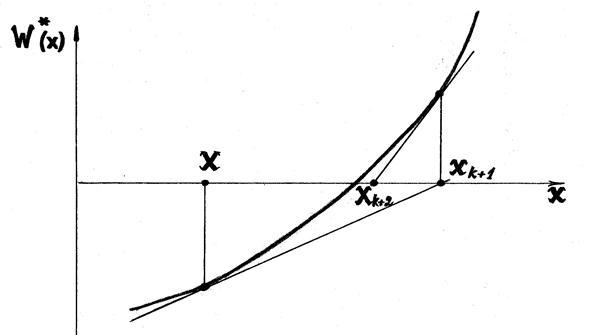
Рис.2. Схема метода касательных
Шаг 1. Следующее приближение к стационарной точке x* определяется по формуле
xk+1 = xk - [W'(xk)/W''(xk)].
Шаг 2. Вычислить W'(xk+1), W''(xk+1)
Шаг 3. Если |W'(xk+1)| < , то закончить поиск. В противном случае необходимо вернуться к шагу 1.
Как явствует из алгоритма, целевая функция W(x) должна быть дважды дифференцируема.
 2015-01-30
2015-01-30 572
572








