| Результаты нахождение оптимума Исходные данные для метода золотого сечения Интервал (a,b): a = 0.0000000000, b = 2.0000000000 EPSILON (точность) E= 9.99999999999612E-0006 Нахождение оптимума по методу "золотого" сечения x = 0.763932022501 a = 0.000000000000 b = 1.236067977499 x = 0.944271909999 a = 0.472135955000 b = 1.236067977499 x = 0.763932022501 a = 0.472135955000 b = 0.944271909999 x = 0.832815729997 a = 0.652475842498 b = 0.944271909999 x = 0.763932022501 a = 0.652475842498 b = 0.832815729997 x = 0.790243257493 a = 0.721359549996 b = 0.832815729997 x = 0.806504495004 a = 0.763932022501 b = 0.832815729997 x = 0.790243257493 a = 0.763932022501 b = 0.806504495004 x = 0.780193260012 a = 0.763932022501 b = 0.790243257493 x = 0.784032017463 a = 0.773982019981 b = 0.790243257493 x = 0.780193260012 a = 0.773982019981 b = 0.784032017463 x = 0.781659534883 a = 0.777820777433 b = 0.784032017463 x = 0.780193260012 a = 0.777820777433 b = 0.781659534883 x = 0.780753327176 a = 0.779287052304 b = 0.781659534883 x = 0.781099467719 a = 0.780193260012 b = 0.781659534883 x = 0.780753327176 a = 0.780193260012 b = 0.781099467719 x = 0.780885541099 a = 0.780539400555 b = 0.781099467719 x = 0.780967253797 a = 0.780753327176 b = 0.781099467719 x = 0.780885541099 a = 0.780753327176 b = 0.780967253797 x = 0.780916752572 a = 0.780835039875 b = 0.780967253797 x = 0.780885541099 a = 0.780835039875 b = 0.780916752572 x = 0.780897462821 a = 0.780866251348 b = 0.780916752572 x = 0.780885541099 a = 0.780866251348 b = 0.780897462821 x = 0.780890094791 a = 0.780878173070 b = 0.780897462821 x = 0.780885541099 a = 0.780878173070 b = 0.780890094791 x = 0.780882726763 a = 0.780878173070 b = 0.780885541099 Минимум найден по методу "золотого" сечения При Xmin = 0.780881857085 значение функции Fmin =-24.369601567218 Количество вычислений k =26 |
Поиск Методом Фибоначчи
Предположим, что нужно определить минимум как можно точнее, т.е. с наименьшим возможным интервалом неопределенности, но при этом можно выполнить только n вычислений функции. Как следует выбрать n точек, в которых вычисляется функция? С первого взгляда кажется ясным, что не следует искать решение для всех точек, получаемых в результате эксперимента. Напротив, надо попытаться сделать так, чтобы значения функции, полученные в предыдущих экспериментах, определяли положение последующих точек. Действительно, зная значения функции, мы тем самым имеем информацию о самой функции и положении ее минимума и используем эту информацию в дальнейшем поиске.
Предположим, что имеется интервал неопределенности (x1; x3) и известно значение функции f (x2 ) внутри этого интервала (см. рис. 2.3.). Если можно вычислить функцию всего один раз в точке x4, то где следует поместить точку x4, для того чтобы получить наименьший возможный интервал неопределенности?
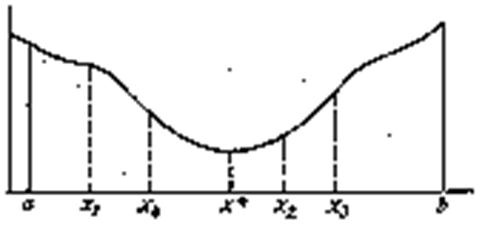
Рисунок 2.3 - Графическое представление функции
Положим x2-x1 = L и x3 -x2 = R, причем L > R, как показано на рис.2.3, и эти значения будут фиксированы, если известны x1, x2 и x3. Если x4 находится в интервале (x1; x2), то:
1.Если f (x4) < f (x2 ), то новым интервалом неопределенности будет (x1;x2) длиной x2- x1=L;
2.Если f (x4) > f (x2 ), то новым интервалом неопределенности будет (x4; x3) длиной x3-x4;
Поскольку не известно, какая из этих ситуаций будет иметь место, выберем x4 таким образом, чтобы минимизировать наибольшую из длин x3-x4 и x2-x1. Достигнуть этого можно, сделав длины x3-x4 и x2-x1 равными, т.е. поместив x4 внутри интервала симметрично относительно точки x2, уже лежащей внутри интервала. Любое другое положение точки x4 может привести к тому, что полученный интервал будет больше L. Помещая x4 симметрично относительно x2, мы ничем не рискуем в любом случае.
Если окажется, что можно выполнить еще одно вычисление функции, то следует применить описанную процедуру к интервалу (x1;x2), в котором уже есть значение функции, вычисленное в точке x4, или к интервалу (x4;x3), в котором уже есть значение функции, вычисленное в точке x2. Следовательно, стратегия ясна с самого начала. Нужно поместить следующую точку внутри интервала неопределенности симметрично относительно уже находящейся там точке. Парадоксально. Но, чтобы понять, как следует начинать вычисления, необходимо разобраться в том, как его следует кончать.
На n-м вычислении n-ю точку следует поместить симметрично по отношению к (n-1)-й точке. Положение этой последней точки в принципе зависит от нас. Для того, чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка xn будет совпадать с точкой xn-1. Однако при этом мы не получаем никакой новой информации. Обычно точки xn-1 и xn отстоят друг от друга на достаточном расстоянии, чтобы определить, в какой половине, левой или правой, находится интервал неопределенности. Они помещаются на расстоянии e/2 по обе стороны от середины отрезка Ln-1; можно самим задать величину e или выбрать эту величину равной минимально возможному расстоянию между двумя точками. (Предположим, что в нашем примере инженер может регулировать температуру интервалом в 1°С, поэтому e =1.)
Интервал неопределенности будет иметь длину Ln, следовательно,
Ln-1=2Ln-e (рис. 2.4, нижняя часть).
На предыдущем этапе точки xn-1 и xn-2 должны быть помещены симметрично внутри интервала Ln-2 на расстоянии Ln-1 от концов этого интервала. Следовательно, Ln-2=Ln-1+ Ln (рис. 2.4, средняя часть).
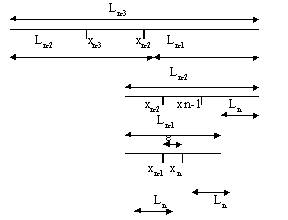
Рисунок 2.4
Замечание. Из рисунка ясно, что на предпоследнем этапе xn-2 остается в качестве внутренней точки.
Аналогично
Ln-3=Ln-2+ Ln-1 (рисунок 2.4, верхняя часть).
В общем случае
Lj-1=Lj+ Lj+1 при 1 < j <n
Таким образом,
Ln-1=2Ln-e,
Ln-2=Ln-1+Ln =3Ln -e
Ln-3=Ln-2+Ln-1=5Ln-2 -e
Ln-4=Ln-3 +Ln-2 =8Ln-3 -e и т.д.
Если определить последовательность чисел Фибоначчи следующим образом:
F0=1, F1=1 и Fk =Fk-1 +F k-2 для k=2,3,...,
то Ln-j =Fj +1Ln-Fj-1 e, j=1,2,...,n-1.
Если начальный интервал (a;b) имеет длину Lj=(b-a), то
Lj=FnLn-Fn-2e,
т.е.
Ln =L1/Fn +e Fn-2/Fn .
Следовательно, произведя n вычислений функции, мы уменьшим начальный интервал неопределенности в 1/Fn раз по сравнению с его начальной длиной (пренебрегая e), и это - наилучший результат.
Если поиск начат, то его несложно продолжить, используя описанное выше правило симметрии. Следовательно, необходимо найти положение первой точки, которая помещается на расстоянии L2 от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии L2 от второго конца интервала:
L2=Fn-1Ln- Fn-3e = Fn-1 L1 /Fn +e (Fn-1 Fn-2 - Fn Fn-3 )/Fn = Fn-1 L1 /Fn +e (-1)n /Fn.
После того как найдено положение первой точки, числа Фибоначчи больше не нужны. Используемое значение e может определяться из практических соображений. Оно должно быть меньше L1 /Fn+1, в противном случае мы будем напрасно тратить время на вычисление функции.
Таким образом, поиск методом Фибоначчи, названный так в виду появления при поиске чисел Фибоначчи, является итерационной процедурой. В процессе поиска интервала (x1; x2 ) с точкой x2, уже лежащей в этом интервале, следующая точка x4 всегда выбирается такой,
что x3 - x4=x2-x1 или
x4 -x1 =x3 -x2, т.е. x4 =x1 -x2 +x3.
Если f (x2 ) = f 2 и f (x4 ) = f 4, то можно рассмотреть четыре случая:
o х4 < x2, f4 < f2 Новый интервал (х1; x2), содержащий точку х4
- х4 > x2, f4 < f2 Новый интервал (х2; x3 ), содержащий точку х4
- х4 < x2, f4 > f2 Новый интервал (х4; x3 ), содержащий точку х4
- х4 > x2, f4 > f2 Новый интервал (х1; x4 ), содержащий точку х4
В приведенной программе реализованы указанные выше случаи. В томвиде, как она приведена здесь, эта программа позволяет производить до 40вычислений функции. В программе исследуется функция f (x)=x4 -14x3+60x2-70x. Методы полиномиальной аппроксимации
Сущность метода. Согласно теоремы Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома.
Рассмотрим следующие вопросы:
1.Квадратичная аппроксимация
2.Кубическая интерполяция
3.Квадратичные функции
Квадратичная аппроксимация
Используется несколько значений функции в определенных точках для аппроксимации функции обычным полиномом по крайней мере в небольшой области значений. Затем положение минимума функции аппроксимируется положением минимума полинома, поскольку последний вычислитель проще.
Простейший случай основан на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть по крайней мере квадратичной.
Если целевая функция W(x) в точках x1, x2, x3 принимает соответствующие значения W1, W2, W3, то можно определить коэффициенты aо, a1, a2 таким образом, что значения квадратичной функции
q(x) = ao + a1(x - x1) + a2(x - x1)(x - x2)
совпадут со значением W(x) в трех указанных точках. Вычислим q(x) в трех указанных точках (см. Табл.2.1).
Таблица 2.1 - Вычисление значений
| W1 = W(x1) =q(x1) = ao | ao = W1 |
| W2 = W(x2) = q(x2) = W1 + a1(x2 - x1) | a1 =(W2 - W1)/(x2 - x1) |
| W3 =q(x3) = W1 + [(W2 - W1) (x3 - x1)]/ /(x2 - x1) + a2(x3 - x1) (x3 - 2) | a2 = 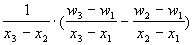
|
 =0 =0
| 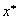 = = 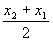 - - 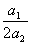
|
Метод Пауэлла
Если извесны значения функции f (x) в трех разных точках равные соответвенно f, f, f, то функция f (x) может быть аппроксимирована квадратичной функцией
(x)=Ax2+Bx+C,
где А, В и С определяются из уравнений
A2+B+C=f A2+B+C=f A2+B+C=f
После преобразований этих уравнений получаем
A=fff B=fff C=fff
где .Ясно, что (x) будет иметь минимум в точке x=-B/2A, если А>0. Cледовательно можно аппроксимировать точку минимума функции f (x) значением
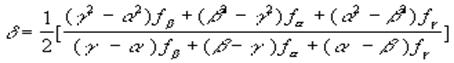
Этод метод может непосредственно применяться к функциям одной переменной. Он может быть очень полезен для выполнения линейного поиска в процедурах, описанных в теме №3. В этих процедурах требуется найти минимум функции f (x) в точках прямой x0+d, где x0- заданная точка, а d определяет заданное направление. Значение функции f (x0+d) на этой прямой является значениями функции одной переменной :
= f (x0+d).
Идеи и результаты, изложенные выше, преобразуются в вычеслительные процедуры, описанные далее. Предположим, что заданы унимодальная функция одной переменной f (x), начальная апроксимация положения минимума и длинна шага D, является величиной того же порядка, что и расстояние от точки А до точки истенного минимума x*(условие, которое не всегда просто удовлетворить). Вычислительная процедура имеет следующие шаги:
Шаг 1. x2 = x1 + D x.
Шаг 2. Вычислить W(x1) и W(x2).
Шаг 3.
o Если W(x1) > W(x2), то x3 = x1 + 2 D x.
- Если W(x1)< W(x2), то x3 = x1 - D x.
W(x1) > W(x2),
Шаг 4. Вычислить W(x3) и найти
Wmin = min{ W(x1),W(x2), W(x3)},
Xmin = xi, соответствующая Wmin.
Шаг 5. По x1, x2, x3 вычислить x*, используя формулу для оценивания с помощью квадратической аппроксимации.
Шаг 6. Проверка окончания
o Если | Wmin - W(x*)| < W, то закончить поиск. В противном случае к шагу 7.
- Если | Xmin - x*| < x, то закончить поиск. В противном случае к шагу 7.
Шаг 7. Выбрать Xmin или x* и две точки по обе стороны от нее. Обозначить в естественном порядке и перейти к шагу 4.
Данный метод часто называют методом Пауэлла, он реализован в программе
Заметим, что если точка Е задана слишком малой, то а также f, f, f будут очень близко друг к другу и значение (см. Уравнение (1)) может стать вообще недостижимыми. Чтобы преодолеть эту трудность, перепишем уравнение(1) для второй и последней интерполяции:
 2015-01-30
2015-01-30 602
602








