Распределение одной сл\в, входящей в систему, найденное при условии, что другая сл\в приняла определенное значение, называется условным законом распределения.
Усл закон распр можно задавать как функцией распределения так и плотностью распределения.
Усл плотность распределения вычисляется по формулам:
 ;
; 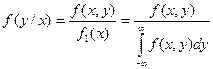 . Усл плотность распр обладает всеми св-ми плотности распределения одной сл\в.
. Усл плотность распр обладает всеми св-ми плотности распределения одной сл\в.
Условным м\о искретной сл\в Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности. 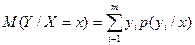
Для непрерывных сл\в:  , где f(y/x) – усл плотность сл\в Y при X=x.
, где f(y/x) – усл плотность сл\в Y при X=x.
Усл м\о M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.
Пример. Найти условное математическое ожидание составляющей Y при X= x1=1 для дискретной двумерной сл\в, заданной таблицей:
| Y | X | |||
| x1=1 | x2=3 | x3=4 | x4=8 | |
| y1=3 | 0,15 | 0,06 | 0,25 | 0,04 |
| y2=6 | 0,30 | 0,10 | 0,03 | 0,07 |
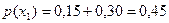 ;
; 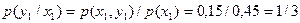
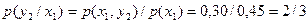
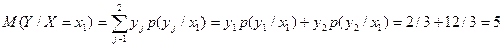
Аналогично определяются усл дисперсия и условные моменты системы сл\в.
28. Неравенство Маркова (лемма Чебышева) с док-вом для дискретной сл\величины. Пример.
Теорема. Если сл\в Х принимет только неотриц знач и имеет мат\о, то для любого положительного числа А верно неравенство: 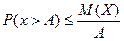 . Доказательство для дискретной сл\в Х: Расположим значения дискр сл\в Х в порядке возрастания, из кот часть значений
. Доказательство для дискретной сл\в Х: Расположим значения дискр сл\в Х в порядке возрастания, из кот часть значений 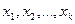 будет не больше числаА, а др часть
будет не больше числаА, а др часть 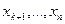 будут больше А, т.е
будут больше А, т.е 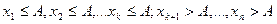
Запишем выражение для м\о M(X): 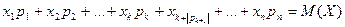 , где
, где 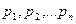
- в-ти т\ч сл\в Х примет значения 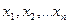 . Отбрасывая первые k неотрицательных слагаемых получим:
. Отбрасывая первые k неотрицательных слагаемых получим: 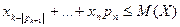 . Заменяя в этом неравенстве значения
. Заменяя в этом неравенстве значения 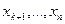 меньшим числом, получим неравенство:
меньшим числом, получим неравенство: 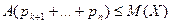 или
или 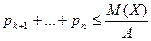 . Сумма в-тей в левой части представляет сумму в-ей событий
. Сумма в-тей в левой части представляет сумму в-ей событий 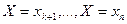 , т.е в-ть соб Х>А. Поэтому
, т.е в-ть соб Х>А. Поэтому 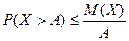 . Т.к события
. Т.к события 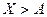 и
и 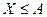 противоположные, то заменяя
противоположные, то заменяя 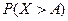 выражением
выражением 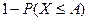 , придём к др форме неравенства Маркова:
, придём к др форме неравенства Маркова: 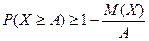 . Неравенство Маркова применимо к любым неотрицательным сл\в.
. Неравенство Маркова применимо к любым неотрицательным сл\в.
29. Неравенство Чебышева для средней арифметической сл\в. Теорема Чебышева с док-м и её значение и пример.
Теорема Чебышева(ср.арифм). Если дисперсии n независимых сл\в 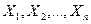 ограничены 1 и той же постоянной, то при неограниченном увеличении числа n ср арифметическая сл\величин сходится по в-ти к средней арифм их м\ожиданий
ограничены 1 и той же постоянной, то при неограниченном увеличении числа n ср арифметическая сл\величин сходится по в-ти к средней арифм их м\ожиданий 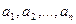 , т.е
, т.е 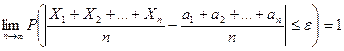 или
или 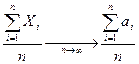 *(над стрелкой Ро- R)
*(над стрелкой Ро- R)
Докажем ф-лу 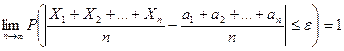 и выясним смысл формулировки «сходимость по в-ти». По условию
и выясним смысл формулировки «сходимость по в-ти». По условию 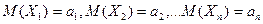 ,
, 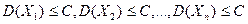 , где С - постоянное число. Получим неравенство Чебышева в форме (
, где С - постоянное число. Получим неравенство Чебышева в форме (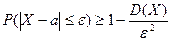 ) для ср арифм сл\в, те для
) для ср арифм сл\в, те для 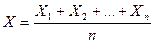 . Найдём м\о M(X) и оценку дисперсии D(X):
. Найдём м\о M(X) и оценку дисперсии D(X): 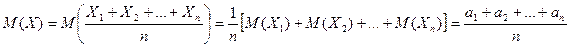 ;
;
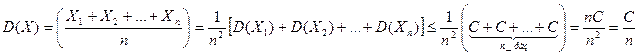 (здесь использованы свойства м\о и дисперсии и т\ч сл\в
(здесь использованы свойства м\о и дисперсии и т\ч сл\в 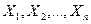 независимы, а след-но, дисперсия их суммы = сумме дисперсий)
независимы, а след-но, дисперсия их суммы = сумме дисперсий)
Запишем неравенство 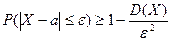 для сл\в
для сл\в 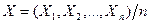 :
:
30. Теорема Чебышева с выводом и его частные случаи для сл\в, распределённой по биномиальному закону, и для частности события.
Неравенство Чебышева. Теорема. Для люб сл\в имеющей м\о и дисперсию, справедливо неравенство Чебышева: 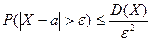 , где
, где 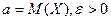 .
.
Применим неравенство Маркова в форме 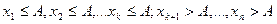 к сл\в
к сл\в 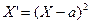 , взяв в кач + числа
, взяв в кач + числа  . Получим:
. Получим: 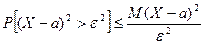 . Т.к неравенство
. Т.к неравенство 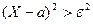 равносильно неравенству
равносильно неравенству 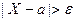 , а
, а 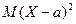 есть дисперсия сл\в Х, то из неравенства
есть дисперсия сл\в Х, то из неравенства 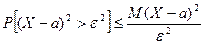 получаем доказываемое
получаем доказываемое 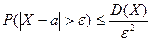 . Учитывая, что события
. Учитывая, что события 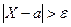 и
и 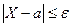 противоположны, неравенство Чебышева можно записать и в форме:
противоположны, неравенство Чебышева можно записать и в форме: 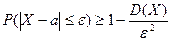 . Неравенство Чебышева применимо для любых сл\в. В форме
. Неравенство Чебышева применимо для любых сл\в. В форме 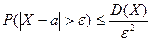 оно устанавливает верхнюю границу, а в форме
оно устанавливает верхнюю границу, а в форме 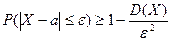 - нижнюю границу в-ти рассм-го события.
- нижнюю границу в-ти рассм-го события.
Запишем неравенство Чебышева в форме 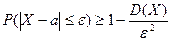 для некоторых сл\в:
для некоторых сл\в:
А) для сл\в Х=m, имеющей биноминальный закон распр с м\о a=M(X)=np и дисперсией D(X)=npq.
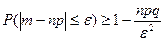 ;
;
Б) для частности m\n события в n независимых испытаниях, в каждом из кот оно может произойти с 1 и той же в-тью 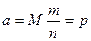 ; и имеющей дисперсию
; и имеющей дисперсию 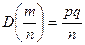 :
: 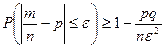 .
.
 2015-01-30
2015-01-30 937
937








