1. Что такое функция?
2. Какая функция называется бесконечно малой, бесконечно большой?
3. Какова связь между бесконечно малой и бесконечно большой функциями?
4. Сформулируйте основные теоремы о пределах.
5. Дайте определение непрерывной функции в точке и на промежутке.
6. Сформулируйте необходимый и достаточный признаки убывания (возрастания) функции на интервале.
6. Что называется экстремумом функции на интервале?
7. Сформулируйте необходимое и достаточное условие существования экстремума.
8. Дайте определения выпуклости и вогнутости кривой на интервале.
9. Что называется точкой перегиба графика функции? Алгоритм нахождения точек перегиба.
10. Сформулируйте достаточный признак существования точки перегиба.
11. Изложите общую схему исследования функции и построения ее графика.
Найти пределы:
1. 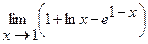 | 2. 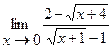 |
3. 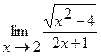 | 4. 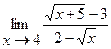 |
5. 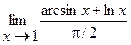 | 6. 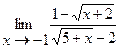 |
7. 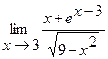 | 8. 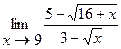 |
9. 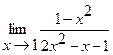 | 10. 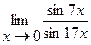 |
11. 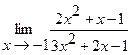 | 12. 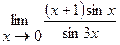 |
13. 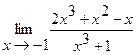 | 14. 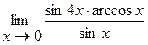 |
15. 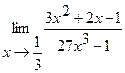 | 16. 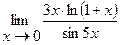 |
17. 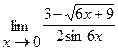 | 18. 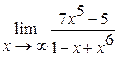 |
19. 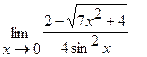 | 20. 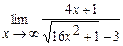 |
21. 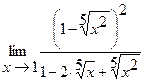 | 22. 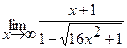 |
23 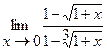 | 24. 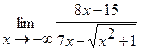 |
25. 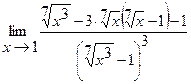 | 26. 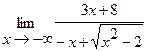 |
27. 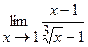 | 28. 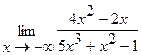 |
29. 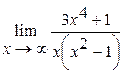 | 30. 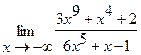 |
VII. ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ ПО ТЕМЕ:
«ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА»
№1 1. 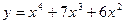 2. 2. 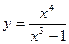 3. 3. 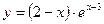 | №2 1. 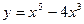 2. 2. 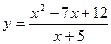 3. 3. 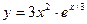 |
№3 1. 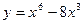 2. 2. 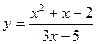 3. 3. 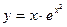 | №4 1. 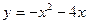 2. 2. 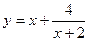 3. 3. 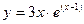  |
№5 1. 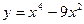 2. 2. 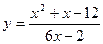 3. 3. 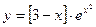 | №6 1. 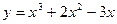 2. 2. 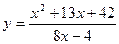 3. 3. 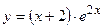 |
№7 1. 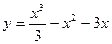 2. 2. 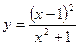 3. 3. 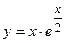 | №8 1. 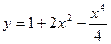 2. 2. 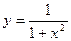 3. 3. 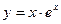 |
№9 1. 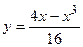 2. 2. 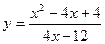 3. 3. 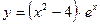 | №10 1. 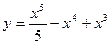 2. 2. 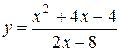 3. 3. 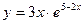 |
№11 1. 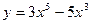 2. 2. 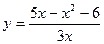 3. 3. 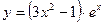 | №12 1. 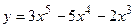 2. 2. 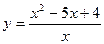 3. 3. 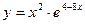 |
№13 1. 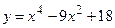 2. 2. 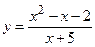 3. 3. 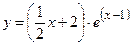 | №14 1. 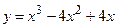 2. 2. 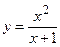 3. 3. 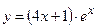 |
№15 1. 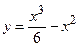 2. 2. 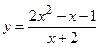 3. 3. 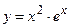 | №16 1. 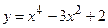 2. 2. 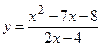 3. 3.  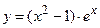 |
№17 1. 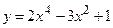 2. 2. 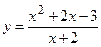 3. 3. 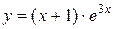 | №18 1. 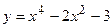 2. 2. 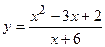 3. 3. 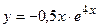 |
№19 1. 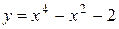 2. 2. 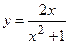 3. 3. 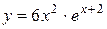 | №20 1. 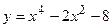 2. 2. 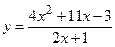 3. 3. 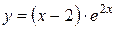 |
№21 1. 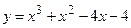 2. 2. 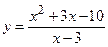 3. 3. 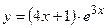 | №22 1. 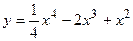 2. 2. 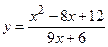 3. 3. 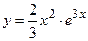 |
№23 1. 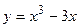 2. 2. 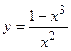 3. 3. 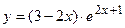 | №24 1. 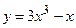 2. 2. 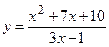 3. 3. 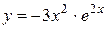 |
VIII. ПРИМЕРНЫЕ ВАРИАНТЫ ТЕСТОВ
1. Функция 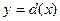 называется бесконечно малой, если
называется бесконечно малой, если
a). 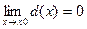
b). 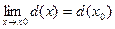
c). 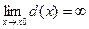
d). 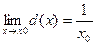
2 Предел 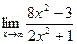 равен
равен
a). 0
b). 1
c). -3
d). 4
3. Предел 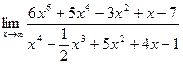 равен
равен
a). ∞
b). 0
c). 1
d). -∞
4 Предел 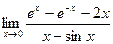 равен
равен
a). 4
b). -1
c). 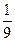
d). 2
5 Предел 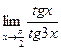 равен
равен
a). 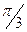
b). 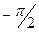
c). 3
d). 4
6 Предел 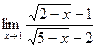 равен
равен
a). -5
b). 2
c). 0,3
d). 0
7. Производная функции 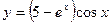 имеет вид
имеет вид
a) 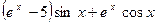
b) 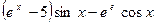
c) 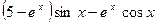
d) 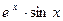
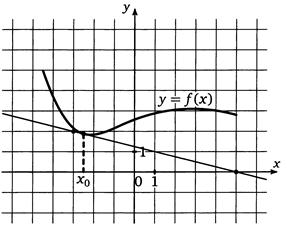
8. На рисунке изображён графc)ик функции 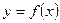 и касательная к нему в тоd)чке с абсциссой
и касательная к нему в тоd)чке с абсциссой 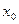 .d)
.d)
Найдите значение производной функции 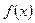 в точке
в точке 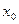 .
.
a) -1
b) -0,5
c) -2
d) -0,25
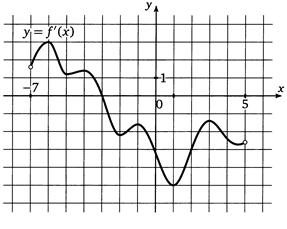
9. На рисунке изображён график производной функции 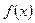 , определённой на интервале (-7; 5). Найдите точку экстремума функции
, определённой на интервале (-7; 5). Найдите точку экстремума функции 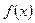 , принадлежащих отрезку [-6; 4]
, принадлежащих отрезку [-6; 4]
a) -1
b) -3
c) -2
d) -4
10 Если при переходе аргумента слева направо через точку 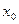 производная
производная 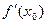 меняет знак с — на +, то функция
меняет знак с — на +, то функция
a) имеет максимум
b) имеет точку перегиба
c) имеет минимум
d) не определена
ЛИТЕРАТУРА
1. Зайцев, И. А. Высшая математика: учебник / И. А. Зайцев. – 3-е изд., испр. - М.: Дрофа, 2004. – 400 с.
2. Данко, П.Е. Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – М.: Оникс, 2008. – 816 с.
3. Кудрявцев, В. А. Краткий курс высшей математики: учеб. пособие / В.А. Кудрявцев, Б. П. Демидович. - М.: АСТ, 2008. – 654с.
4. Минорский, К. П. Сборник задач по высшей математике: учеб. пособие /
К. П. Минорский. - 15-е изд. –М.: Физматлит, 2008. – 336 с.
5. Письменный, Д.Т. Конспект лекций по высшей математике: (в2 ч.) Ч.1 / Д. Т. Письменный. - 7-е изд. –М.: Айрис-пресс, 2007. – 288 с.
 2015-01-07
2015-01-07 1293
1293







