Решение. Найдем минор второго порядка, отличный от нуля, и зафиксируем его

М₂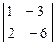^¢ = = 0, М₂^² = 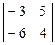¹ 0.

Для минора М₂^² ¹ 0 окаймляющими будут только два минора:

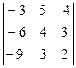М₃ = = 0, М₃^* = = 0,

каждый из которых равен нулю. Поэтому ranq А = 2, а указанный минор М₂^² может быть принят за базисный.

Пример 2. Найти ранг матрицы А методом элементарных преобразований

А =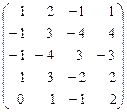

Решение. Постараемся привести матрицу к треугольному виду, получив под главной диагональю нули. Сначала получим нули в первом столбце. Для этого к четвертой строке прибавим первую, умноженную на (-1), а к третьей и второй прибавим первую строку. Получим:

А ~ .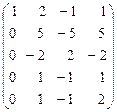

Вторая, третья и четвертая строки оказались пропорциональными. Это значит, в любых двух из этих строк можно получить нули, а именно:

А ~ . ~

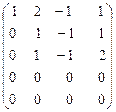
Вычтем из третьей строки вторую, получим:

А. ~ ~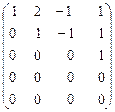

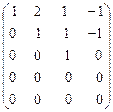
М₃ = 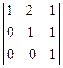¹ 0, следовательно, ranq A = 3.