Пример 1. Найти матрицу, обратную матрице
А = 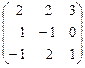
и сделать проверку.
Решение. 1. det A = 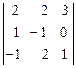 = 2
= 2 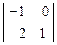 - 2
- 2 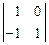 +
+
+ 3 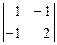 = 2 × (-1) – 2 × 1 + 3 × 1 = -1 ¹ 0, следовательно, существует А-1.
= 2 × (-1) – 2 × 1 + 3 × 1 = -1 ¹ 0, следовательно, существует А-1.
2. Найдем союзную матрицу А*:
А11 = 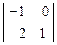 = -1; А12 = -
= -1; А12 = - 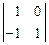 = -1; А13 =
= -1; А13 = 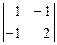 = 1;
= 1;
А21 = - 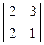 = 4; А22 =
= 4; А22 = 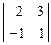 = 5; А23 = -
= 5; А23 = - 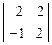 = -6;
= -6;
А31 = 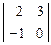 = 3; А32 = -
= 3; А32 = - 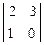 = 3; А33 =
= 3; А33 = 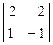 = -4.
= -4.
А* = 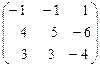 .
.
3. Транспонируем матрицу А*:
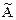 = А*т =
= А*т = 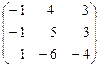 .
.
4. Получаем матрицу А-1:
А-1 = 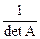
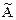 =
= 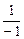
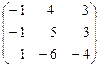 =
= 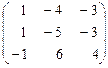 .
.
Сделаем проверку: А × А-1 = А-1 × А = Е.
А × А-1 = 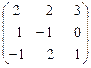
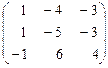 =
=
= 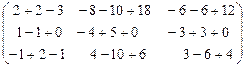 =
= 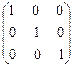 = Е.
= Е.
Итак, обратная матрица найдена верно.
Пример 2. Решить систему уравнений матричным способом:
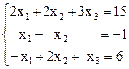
Решение. Рассмотрим три матрицы: А – основная матрица системы, Х – матрица-столбец неизвестных х1, x2, x3, В – матрица-столбец свободных членов:
А = 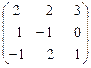 , X =
, X = 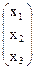 , B =
, B = 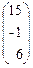 .
.
Пользуясь правилом умножения матриц, система может быть записана в матричной форме:
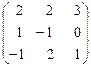
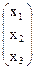 =
= 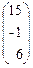
или А × Х = В. Отсюда Х = А-1 ×В. Матрица А-1 найдена в предыдущем примере. Решение в матричной форме запишется так:
Х = 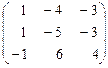
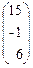 =
= 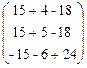 =
= 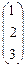 .
.
Итак, решение данной системы: х1 = 1, х2 = 2, x3 = 3.
Пример 3. Решить уравнение
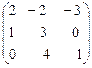 × Х =
× Х = 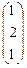 .
.
Решение. Это уравнение вида А × Х = В, решение которого Х = А-1 × В.
Найдем матрицу А-1:
1. det A = 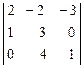 =
= 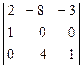 = -
= - 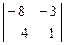 =
=
= - (-8 + 12) = -4 ¹ 0, следовательно, матрица А-1 существует.
2. Составим матрицу А*:
А11 = 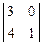 = 3 А12 = -
= 3 А12 = - 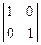 = -1 А13 =
= -1 А13 = 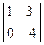 = 4
= 4
А21 = - 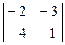 = -10 А22 =
= -10 А22 = 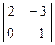 = 2 А23 = -
= 2 А23 = - 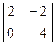 = -8
= -8
А31 = 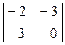 = 9 А32 = -
= 9 А32 = - 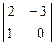 = -3 А33 =
= -3 А33 = 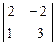 = 8
= 8
А* = 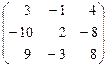 .
.
3. 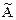 =
= 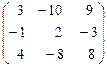 . 4. А-1 = -
. 4. А-1 = - 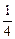
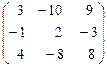 .
.
Найдем теперь матрицу Х:
X = - 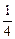
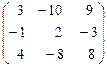
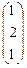 = -
= - 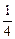
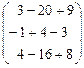 = -
= - 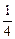
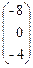 =
= 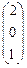 .
.
Ответ. Х = 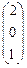 .
.
 2015-01-07
2015-01-07 1058
1058
