В задачах 1 – 7 исследовать систему на совместность и, если она совместна, найти ее общее решение.
1. 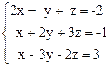 2.
2. 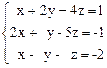
3. 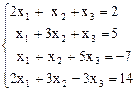 4.
4. 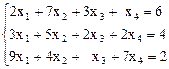
5. 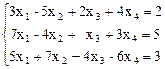 6.
6. 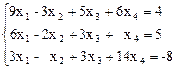
7. 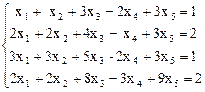
Ответ. 1) система несовместна; 2) r = 2, x = -1 – 2 t,
y = 1 + t, z = t; 3) r = 3, x1 = 1, x2 =2, x3 = -2; 4) r = 2,
x1 = 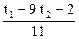 , x2 =
, x2 = 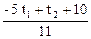 , x3 = t1, x4 = t2;
, x3 = t1, x4 = t2;
5) cистема несовместна; 6) r =2, x1 = t1, x2 = t2,
x3 = 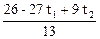 , x4 =
, x4 = 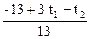 , 7) система несовместна.
, 7) система несовместна.
В задачах 8 – 13 найти общее решение следующих однородных систем:
8. 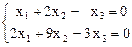 9.
9. 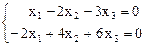
10. 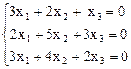 11.
11. 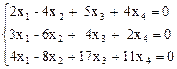
12. 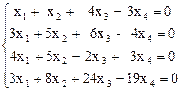 13.
13. 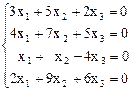
Ответ. 8) t (3, 1, 5); 9) (2 t1 + 3 t2, t1, t2); 10) (0, 0, 0);
11) (t1, t2, - 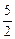 t1 + 5 t2,
t1 + 5 t2, 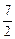 t1 - 7 t2); 12) (8 t1 - 7 t2, - 6 t1 + 5 t2,
t1 - 7 t2); 12) (8 t1 - 7 t2, - 6 t1 + 5 t2,
t1, t2); 13) (0, 0, 0).
В задачах 14 – 19 решить системы:
14. 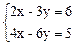 15.
15. 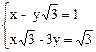
16. 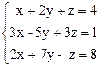 17.
17. 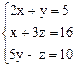
18. 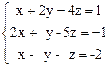 19.
19. 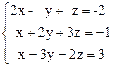
Ответ. 14) не имеет решения; 15) имеет бесконечно много решений: x = t, y = 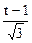 ; 16) x = y = z = 1; 17) x = 1, y = 3,
; 16) x = y = z = 1; 17) x = 1, y = 3,
z = 5; 18) имеет бесконечно много решений: x = 2 t – 1,
y = t + 1, z = t; 19) не имеет решений.
В задачах 20 - 25 найти все решения однородной системы двух линейных уравнений с тремя неизвестными:
20. 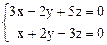 21.
21. 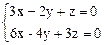
22. 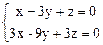 23.
23. 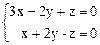
24. 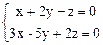 25.
25. 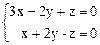
Ответ. 20) х = -2 t, y = 7 t, z = 4 t;
21) х = 2 t, y = 3 t, z = 0;
22) х = 0, y = t, z = 3 t;
23) х = 0, y = t, z = 2 t;
24) х = t, y = 5 t, z = 11 t;
25) х = 3 t, y = 4 t, z = 11 t.
Варианты проверочных работ
Исследовать систему на совместность и, если она совместна, найти ее общее решение.
1. 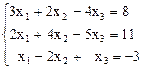 2.
2. 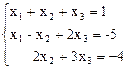
Ответ. 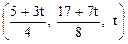 . Ответ.
. Ответ. 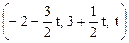 .
.
3. 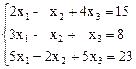 4.
4. 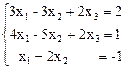
Ответ. (-7 + 3 t, 10 t – 29, t). Ответ. 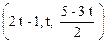 .
.
5. 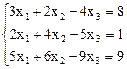 6.
6. 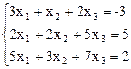
Ответ. 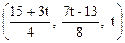 . Ответ.
. Ответ. 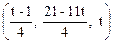 .
.
7. 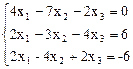 8.
8. 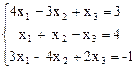
Ответ. (21 + 11 t, 12 + 6 t, t). Ответ. 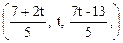 .
.
9. 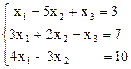 10.
10. 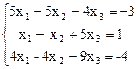
Ответ. 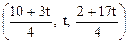 . Ответ.
. Ответ. 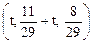 .
.
 2015-01-07
2015-01-07 873
873








