Решение задач. Решение. Запишем расширенную матрицу системы

Пример 1. Решить систему

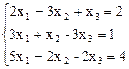
Решение. Запишем расширенную матрицу системы

А_р =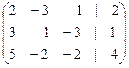

Приведем ее к треугольному виду. Для этого поменяем третий и первый столбцы местами; затем умножим первую строку на 3 и прибавим ко второй; после чего умножим первую строку на 2 и прибавим к третьей и, наконец, из третьей строки вычтем вторую:

А_р ~ ~ ~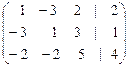

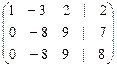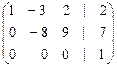
Теперь ясно, что ranq A = 2, а ranq A_р = 3. Согласно теореме Кронекера - Капелли из того, что ranq A ¹ ranq A_р, cледует несовместность данной системы.

Подчеркнем, что, вычисляя ранг матрицы А_р, мы поменяли столбцы местами. Эта операция изменила, вообще говоря, эквивалентность системы.

Пример 2. Решить систему методом Гаусса:

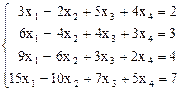
Решение. Запишем расширенную матрицу системы

А_р =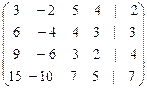

Приведем ее к виду трапеции. Подчеркнем, что при этом следует проводить только линейные преобразования над строками, перечисленными в 1.10 темы 5, дабы сохранить эквивалентность системы (т.е. чтобы не изменить множество ее решений). Первую строку умножим на –2 и прибавим ко второй; первую строку умножим на –3 и прибавим к третьей; первую строку умножим на –5 и прибавим к четвертой. Получим:

А_р ~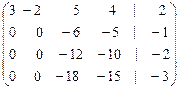

Вторая, третья и четвертая строки пропорциональны, поэтому две из них можно отбросить. Это получилось потому, что соответствующие уравнения системы являются линейно зависимыми и два последних уравнения не несут новой информации о связи между неизвестными, а получаются из второго уравнения путем элементарных преобразований. Заметим, что и два первых столбца линейно зависимы, но отбрасывать один из них нельзя, чтобы не потерять одно из неизвестных системы. Итак,

А_р ~ .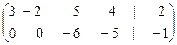

Поэтому ranq A = 2 = ranq A_p. Вывод:

1) система совместна;

2) ranq A = 2 < 4 = n, поэтому система неопределенна;

3) система

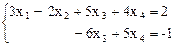
эквивалентна заданной.

В качестве базисного минора выберем минор

М₂ = 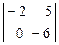= 12 ¹ 0. Переменные х₂ и х₃ – базисные; переменные х₃ и х₄ – свободные.

Базисные переменные оставляем в левой части уравнений, свободные переносим в правую часть. Эквивалентная система принимает вид:

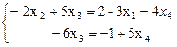
Проводим обратный ход метода Гаусса: из последнего уравнения находим х₃:

х₃ = 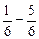х₄.

Подставляем х₃ в первое уравнение и находим х₂:

-2х₂ + 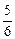- 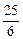х₄ = 2 – 3х₁ –4х₄

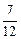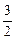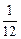х₂ = - + х₁ - х₄.

Решение системы запишется в виде:

Х =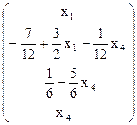

Получили решение, в котором базисные неизвестные выражаются через свободные.

Можно в качестве свободных неизвестных взять произвольные числовые значения t₁, t₂ и записать общее решение системы

Х _общ. =

Придавая свободным неизвестным t₁, t₂ произвольные значения и вычисляя соответствующие значения базисных неизвестных, получаем каждый раз новое частное решение системы. Например, пусть t₁ = 6, t₂ = -7, тогда частное решение

Х_частн. =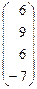

Таких частных решений бесконечное множество.

Пример 3. Найти общее решение однородной системы уравнений.

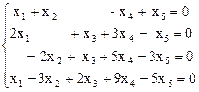
Решение. Запишем основную матрицу системы

А =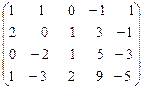

Приведем ее к треугольному виду. Для этого: первую строку умножим на –2 и прибавим ко второй; из четвертой строки вычтем первую. Имеем:

А ~ .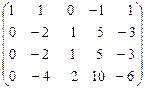

Три последние строки линейно зависимые, вычеркиваем третью и четвертую. Получаем:

А ~ .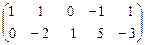

Следовательно, ranq A = 2. Значит, ranq A = 2 < 5 = n и система неопределенна. В качестве базисного выберем минор

М₂ = 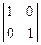= 1 ¹ 0.

Переменные х₁ и х₃ – базисные, х₂, x₄ и x₅ – свободные. Эквивалентная система:

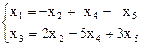
Взяв в качестве свободных неизвестных произвольные числовые значения t₂, t₄, t₅, получим общее решение системы:

Х =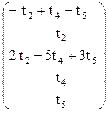

Пример 4. Решить однородную систему двух линейных уравнений с тремя неизвестными x, y, z:

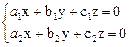
Решение. Предположим, что хотя бы один из определителей, составленный из коэффициентов при неизвестных:

, , ,

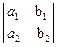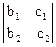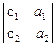например, определитель 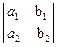отличен от нуля. Тогда его можно принять за базисный минор; переменные х и у будут при этом базисными, а переменная z – свободной.

Оставляем базисные переменные в левой части, а свободную переносим в правую часть:

.

Методом Крамера найдем выражение базисных неизвестных через свободную:

х = 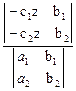= - 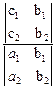z = z,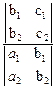

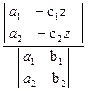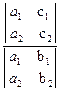y = = - z.

Поэтому общее решение заданной системы можно записать в виде

.

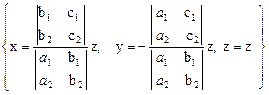Обозначим отношение 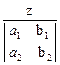через t. Тогда общее решение заданной системы примет вид:

(**)

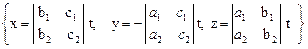Получая это решение, мы предполагали, что 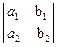¹ 0. Если этот определитель равен нулю, а 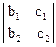¹ 0 или

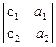¹ 0, рассуждения отличаются лишь переменой ролей неизвестных. Совокупность всех решений снова запишется в виде (**). Если все три последние определителя равны нулю, то коэффициенты уравнений заданной системы пропорциональны, т.е. одно уравнение есть следствие другого и решение системы сводится к решению одного уравнения с тремя неизвестными. Такое уравнение имеет бесчисленное множество решений. Для их нахождения надо двум неизвестным придавать произвольные значения, а третье выбирать так, чтобы при этом удовлетворялось уравнение.

Пример 5. Решить систему

.

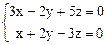Решение. Это однородная система двух уравнений с тремя неизвестными, причем 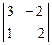= 6 + 2 = 8 ¹ 0. Поэтому ее решение имеет вид (**) из предыдущего примера. Заметим, что определители второго порядка, которые участвуют в записи общего решения, получаются из матрицы 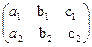вычеркиванием первого (соответственно второго (третьего)) столбца.

Вычеркивая поочередно столбцы матрицы 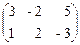, получим множество решений:

х = 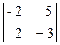× t = -4 t, y = - 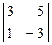= 14 t,

z = 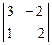× t = 8 t.

Ответ. х: у: z = -2: 7: 4.