2015-01-07
740
Номер варианта второго задания: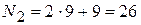 
. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу вариант №6.
1 Решение систем линейных уравнений методами Крамера и Гаусса
Пусть дана система n уравнений с n неизвестными:
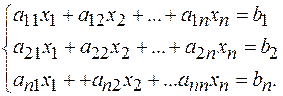
Основная матрица А такой системы квадратная. Определитель этой матрицы
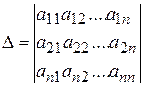
называется определителем системы.
Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.
В дальнейшем мы будем иметь дело только с такими системами.
Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.
Формулы Крамера имеют вид: 
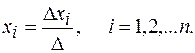(1.1.1)
Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.
Решение осуществляется в два этапа: 1) система приводится к треугольному виду, 2) последовательно определяют неизвестные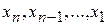 
.
Пример 1.
Решить систему уравнений методами Крамера и Гаусса:
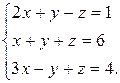
Решение:
а) Метод Крамера.
Найдем определитель системы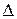 
, 
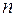. Предварительно сложив второй столбец с третьим и разложив определитель по элементам последнего столбца.
= 
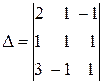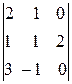=2(-1)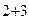 
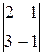=-2(-2-3)=10 
.
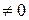Так как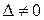 
, то система имеет единственное решение.
Найдем определител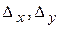и 
и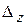 
, заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов (при вычислении определителя 
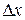преобразования аналогичные предыдущему.)
= 
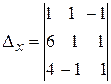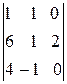=2(-1) 
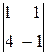-2(-1-4)=10.
При вычислении определителя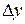 
последнюю строку складываем с первой и вычитаем из второй строки. Разлагаем по элементам последнего столбца.
= 
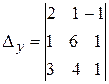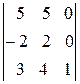=1(-1)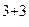 
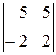=10+10=20.
При вычислении определителя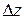 
последнюю строку складываем с первой и со второй строки и разлагаем получившийся определитель по элементам второго столбца.
= 
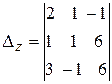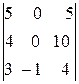=-1(-1)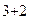 
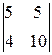=50-20=30.
Подставляя найденные значения в формулы (1.1.1), получим:
х=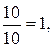 
у= 
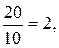z=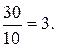 
б) Метод Гаусса.
Составим расширенную матрицу системы:
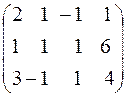
Разрешающим элементом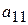 
удобно иметь единицу, поэтому переставим второе уравнение на место первого.
Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.
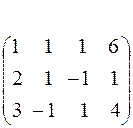(-2) (-3)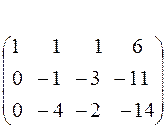 
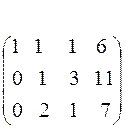
С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.
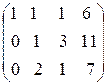(-2)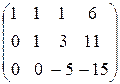 
.
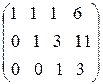Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:
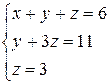
Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у=11-3z=11-9=2. Затем из первого уравнения найдем
х=1, у=2, z=3.
1. Что называется определителем системы?
2. Когда система линейных уравнений имеет единственное решение?
3. Напишите формулы Крамера для решения системы трех линейных уравнений с тремя неизвестными.
4. В чем заключается основная идея метода Гаусса?
5. Какой из рассмотренных методов решения системы линейных уравнений показался Вам более простым?
