Нормальный закон распределения. Нормальное распределение (иногда называемое законом Гаусса) играет исключительно важную роль в теории вероятностей и математической статистике и занимает

Нормальное распределение (иногда называемое законом Гаусса) играет исключительно важную роль в теории вероятностей и математической статистике и занимает среди других законов распределения особое положение. Это объясняется целым рядом причин:

1 Многие случайные величины имеют нормальное или близкое к нормальному распределение.

2 Нормальное распределение хорошо подходит в качестве аппроксимации других распределений (например, биномиального).

3 Нормальное распределение обладает рядом математических свойств, во многом обеспечивших его широкое применение в теории вероятностей и математической статистике.

Случайная величина X называется распределенной по нормальному закону, если ее плотность распределения вероятностей задается формулой

,

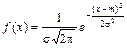где s > 0 и m – параметры распределения.

Так как f (x) > 0 и

,

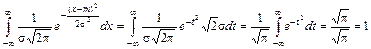то приведенное выше определение корректно. (При проведении преобразований была сделана подстановка 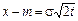, и в результате получили интеграл Пуассона, который равен .)

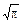Основные свойства нормального распределения:

1 Нормальное распределение полностью определяется двумя параметрами: m и s. Вероятностный смысл этих параметров таков: m – математическое ожидание, s – среднее квадратическое отклонение рассматриваемой случайной величины. То есть для нормального распределения:

M [ X ] = m; D [ X ] = s²; s[ X ] = s.

2 Кривая нормального распределения имеет колоколообразную форму, симметричную относительно прямой x = m, и при x ® –¥ и x ® ¥ эта кривая асимптотически приближается к оси абсцисс.

Общий вид графика функции плотности распределения вероятностей f (x) для произвольных значений параметров m и s изображен на рисунке 19.

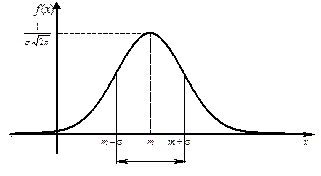
Рисунок 19 – График функции f (x) нормально распределенной
случайной величины

3 Как видно из графика функции f (x), для нормально распределенной случайной величины вероятность получения значений, значительно удаленных от среднего значения m, быстро уменьшается с ростом величины отклонения.

4 Медиана и мода случайной величины, распределенной по нормальному закону, совпадают и равны математическому ожиданию m, x _mod = x _mеd == M [ X ] = m.

5 Коэффициенты асимметрии и эксцесса нормально распределенной случайной величины равны нулю: A [ X ] = 0; Eх [ X ] = 0.

Тот факт, что случайная величина X распределена по нормальному закону с параметрами m и s, символически записывается X ~ N (m; s). Этой случайной величине соответствует следующая функция распределения вероятностей

.

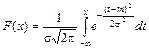График функции распределения F (x) изображен на рисунке 20.

На рисунках 21 и 22 изображены графики функции f (x), соответствующие различным значениям параметров m и s.

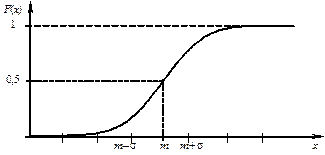
Рисунок 20 – График функции распределения F (x) нормально распределенной случайной величины

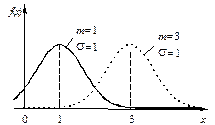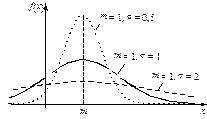Рисунок 21 – График функции f (x) нормально распределенной случайной величины	Рисунок 22 – График функции f (x) нормально распределенной случайной величины