Для вычисления вероятностей событий воспользоваться классическим методом определения вероятностей.
2.1–2.5. Бросают две игральные кости. Вычислить вероятность того, что:
а) сумма очков на верхних гранях превысит k;
б) на обеих костях выпадет разное число очков;
в) произведение очков поделится на k.
| № варианта | k |
2.6–2.10. Из трех карточек с цифрами 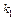 ,
, 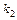 ,
, 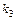 произвольным образом выбирают
произвольным образом выбирают 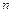 и укладывают на стол в порядке их появления. Предполагая, что все возможные исходы данного опыта равновероятны, найти вероятность того, что полученное таким образом число будет:
и укладывают на стол в порядке их появления. Предполагая, что все возможные исходы данного опыта равновероятны, найти вероятность того, что полученное таким образом число будет:
а) четное;
б) нечетное;
в) кратно 2.
| № варианта | 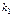 | 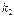 | 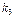 | 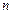 |
2.11–2.15. При наборе телефонного номера абонент набирает 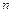 последние цифры наугад. Найти вероятность того, что номер будет набран правильно с первой попытки, если абонент помнит, что цифры разные и номер состоит из
последние цифры наугад. Найти вероятность того, что номер будет набран правильно с первой попытки, если абонент помнит, что цифры разные и номер состоит из 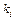 , (
, (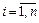 ) цифр.
) цифр.
| № варианта | 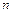 | 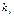 , ( , (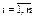 ) ) |
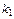 = 1, = 1, 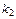 = 2, = 2, 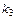 = 3 = 3 | ||
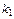 = 1, = 1, 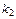 = 3, = 3, 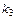 = 8, = 8, 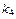 = 5 = 5 | ||
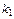 = 7, = 7, 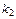 = 3, = 3, 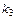 = 5 = 5 | ||
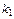 = 4, = 4, 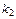 = 3, = 3, 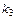 = 8 = 8 | ||
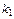 = 3, = 3, 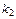 = 5, = 5, 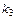 = 6, = 6, 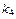 = 7 = 7 |
2.16–2.20. Слово составлено из карточек, на которых написана одна буква. Карточки смешивают и вынимают все по одной без возвращения. Найти вероятность того, что карточки с буквами вынимаются в порядке расположения букв заданного слова.
| № варианта | Слово |
| Мел | |
| Пол | |
| Час | |
| Сто | |
| Дело |
2.21–2.25. Подбрасываются 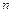 монет. Какова вероятность того, что:
монет. Какова вероятность того, что:
а) хотя бы одна монета упадет кверху гербом;
б) герб выпадет только на  монетах?
монетах?
| № варианта | 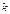 | 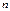 |
2.26–2.30. Участники жеребьевки тянут из ящика жетоны с номерами от 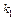 до
до 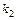 . Найти вероятность того, что номер первого, наудачу извлеченного жетона, будет:
. Найти вероятность того, что номер первого, наудачу извлеченного жетона, будет:
а) нечетным;
б) меньше 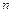 .
.
| № варианта | 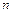 | 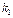 , , 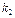 |
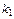 =1, =1, 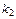 =20 =20 | ||
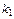 = 10, = 10, 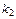 =25 =25 | ||
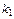 = 1, = 1, 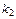 = 100 = 100 | ||
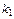 = 1, = 1, 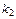 = 50 = 50 | ||
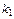 = 50, = 50, 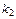 =100 =100 |
 2015-01-07
2015-01-07 1044
1044








