Нормированным (или стандартизованным) нормальным распределением называется нормальное распределение с параметрами m = 0 и s = 1.
Известно, что если случайная величина X распределена нормально с параметрами m и s, то величина Z = (X – m)/s также распределена нормально, но с параметрами m = 0, s = 1 (то есть Z ~ N (0; 1)). Нормирование распределения ведет просто к перенесению начала координат в центр распределения, то есть к «центрированию», и к масштабированию оси абсцисс в долях s.
Функция плотности распределения вероятностей стандартного распределения
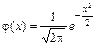 .
.
В приложении A приведены значения этой функции для неотрицательных значений аргумента, график функции j(x) изображен на рисунке 23.
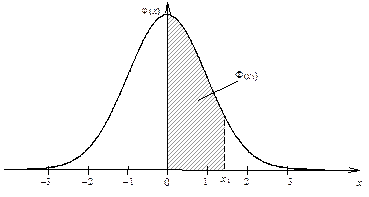
Рисунок 23 – График функции j(x)
Вычислим для нормально распределенной случайной величины X вероятность попадания на участок от a до b:
 .
.
Сделав в интеграле замену переменной t = (x – a)/s (то есть «нормируя» случайную величину) и, соответственно, изменяя пределы интегрирования, получим
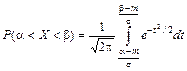 .
.
Как известно, неопределенный интеграл 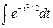 не выражается через элементарные функции, но его можно выразить через специальную функцию
не выражается через элементарные функции, но его можно выразить через специальную функцию
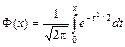 , (27)
, (27)
называемую функцией Лапласа (или «интегралом вероятностей»), для которой составлены таблицы значений. В геометрической интерпретации Ф(x) равна площади фигуры под кривой j(x), опирающейся на отрезок [0; x ]. На рисунке 23 это фигура выделена штриховкой.
В приложении Б приведены значения функции Лапласа для положительных значений x. Функция F(x) – нечетная, то есть F(– x) = – F(x); при x > 5 можно принять F(x) = 0,5.
С помощью функции Лапласа вероятность попадания нормально распределенной случайной величины X на участок от a до b выражается формулой
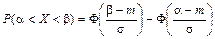 . (28)
. (28)
Формула для расчета вероятности отклонения нормально распределенной случайной величины Х от своего математического ожидания на величину 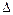 имеет вид:
имеет вид:
 . (29)
. (29)
Примеры случайных величин, распределенных по нормальному закону.
Известно, что нормально распределенные случайные величины широко распространены на практике. Нормальное распределение возникает в тех случаях, когда складывается большое число независимых (или слабо зависимых) случайных величин X 1, X 2, …, Xn:
 ,
,
причем эти величины сравнимы по порядку своего влияния на рассеивание суммы. Тогда, каковы бы ни были законы распределения отдельных величин Хi, закон распределения их суммы X будет близок к нормальному, причем тем ближе, чем больше число слагаемых n. На практике наиболее часто встречаются именно такие случайные величины.
Результаты измерения длины, массы, времени, ошибки измерения и многие другие случайные величины имеют нормальное или близкое к нормальному распределение.
Рассмотрим пример. Пусть производятся измерения некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат испытания оказывают влияние очень многие, не зависящие друг от друга случайные факторы: температурные колебания в помещении, воздействия окружающей среды, неточность измерительной шкалы, смена контрольного персонала и т. д.
В зависимости от источников появления ошибок различают систематические и случайные ошибки.
К систематическим ошибкам относятся, например, односторонние отклонения, вызванные, скажем, изменением настройки измерительного прибора или сменой контрольного персонала. Эти ошибки можно устранить путем систематического изучения причины их возникновения.
Случайные ошибки вызваны влиянием множества различных неконтролируемых причин: температурных колебаний, влажности, вибраций в окружающей среде и т. п. Каждый из этих факторов порождает ничтожную «частную ошибку». Но поскольку число этих факторов очень велико, совокупное их действие порождает уже заметную «суммарную ошибку». Полностью исключить воздействие этих факторов невозможно, так как нельзя заранее предусмотреть степень их влияния на результат конкретного измерения. Подобные случайные ошибки вызывают при измерениях отклонения в обе стороны от истинного значения.
Рассматривая общую ошибку как сумму очень большого числа взаимно независимых частных ошибок, мы вправе заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.
Пример 39 Случайная величина X распределена по нормальному закону с параметрами M [ X ] = m, s[ X ] = s. Найти вероятность того, что случайная величина X будет принимать значения, удаленные от математического ожидания не более чем на: а) s, б) 2s, в) 3s.
Решение. Для вычисления искомых вероятностей воспользуемся формулой (28):
а) 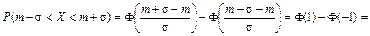
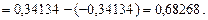
Произведем расчет, используя формулу (29):
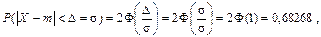
где 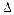 =
= 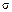 – величина отклонения случайной величины Х от ее математического ожидания.
– величина отклонения случайной величины Х от ее математического ожидания.
На рисунке 24 под графиком кривой нормального распределения указаны площади фигур, ограниченных кривой f (x) и осью абсцисс, которые равны вероятностям попадания значения случайной величины на указанные отрезки. График функции распределения F (x) изображен на рисунке 25.
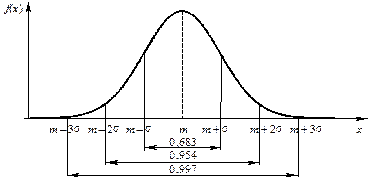
Рисунок 24 – Вероятность того, что случайная величина X будет принимать значения, удаленные от математического ожидания не более чем на: а) s, б) 2s, в) 3s
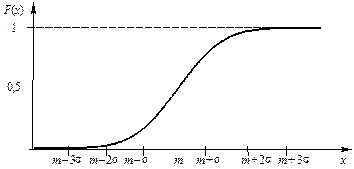
Рисунок 25 – График функции распределения F (x)
нормально распределенной случайной величины
б) 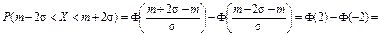
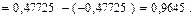
в) 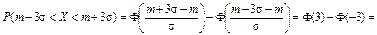

Пример 40 Случайное отклонение изменения курса акций некоторой компании относительно их текущего курса является случайной величиной, распределенной по нормальному закону со средним квадратическим отклонением, равным 5 у.е. Систематические отклонения изменения курса акций от номинальной стоимости отсутствуют. Какова вероятность того, что в определенный день курс акции отклонится от номинала не более чем на 2 у. е.? Какова вероятность того, что в определенный день курс акции отклонится от номинала более чем на 2 у. е.?
Решение. Рассмотрим случайную величину X – отклонение изменения курса акций некоторой компании относительно их текущего курса. Согласно условию, M [ X ] = 0 [у. е.], s[ X ] = 5 [у. е.]. Найдем вероятность события A ={в определенный день курс акции отклонится от номинала не более чем на 2 у. е.}:

Найдем вероятность события В = {в определенный день курс акции отклонится от номинала более чем на 2 у. е.}:
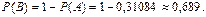
На рисунке 26 штриховкой выделена фигура, площадь которой равна вероятности события В.
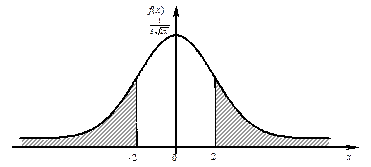
Рисунок 26 – График плотности распределения вероятностей
нормального закона
Вопросы для самоконтроля
1 Какими параметрами определяется биномиальный закон распределения?
2 Какими параметрами определяется геометрический закон распределения?
3 Какими параметрами определяется закон Пуассона?
4 Приведите примеры случайных величин, распределенных по равномерному закону.
5 Какими параметрами определяется показательный закон распределения?
6 Какими параметрами определяется нормальный закон?
7 Как определяется вероятность попадания значения случайной величины, распределенной нормально, в некоторый интервал?
8 Чему равны мода, медиана, математическое ожидание случайной величины, распределенной по нормальному закону?
ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
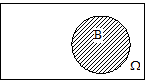
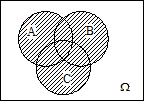
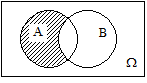
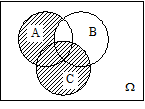
Задача 1 Эксперимент состоит в том, что внутри прямоугольника W, изображённого на рисунке 27, случайным образом выбирается точка. События A, B и C состоят, соответственно, в попадании выбранной точки внутрь кругов A, B и C. Изобразить области, попадание в которые соответствует осуществлению событий:
а) 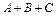 ;
;
б) 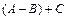 ;
;
в) 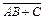 ;
;
г) 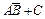 .
.
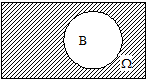
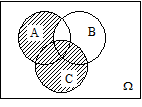
Решение. Области, попадание в которые соответствует осуществлению указанных событий, приведены на следующих рисунках:
а) 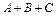
 |  |
| А | 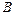 |
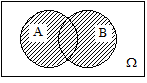 |  |
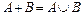 | 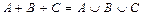 |
б) 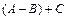
 |  |
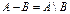 | 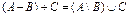 |
| Рисунок 27 (начало) – Диаграммы Эйлера-Венна для событий |
в) 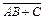
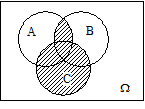 | 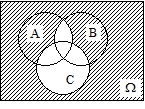 |
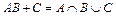 | 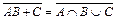 |
г) 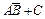
 |  |
| А | 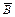 |
 |  |
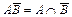 | 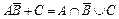 |
| Рисунок 27 (окончание) |
Задача 2 При наборе телефонного номера абонент набирает 2 последние цифры наугад. Найти вероятность того, что номер будет набран правильно с первой попытки, если:
а) абонент помнит, что цифры разные и нечетные;
б) абонент помнит, что цифры нечетные.
Решение. а) Элементарными исходами рассматриваемого эксперимента являются возможные варианты последовательного набора двух цифр из пяти. Так как в условии указано, что цифры нечетные и разные, то выбирать будем две цифры из 1, 3, 5, 7, 9.
Пространство элементарных исходов рассматриваемого эксперимента:
W = {(1, 3), (1, 5), (1, 7), (1, 9), (3, 1), (3, 5), (3, 7), (3, 9), (5, 1), (5, 3), (5, 7), (5, 9), (7, 1), (7, 3), (7, 5), (7, 9), (9, 1), (9, 3), (9, 5), (9, 7)}.
В данном случае пространство элементарных исходов состоит из 20 элементов: n = 20.
Поскольку цифры набираются случайным образом, все элементарные исходы равновозможны, то для вычисления вероятности интересующего нас события можно воспользоваться классическим методом определения вероятностей.
Число исходов, благоприятных событию A, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
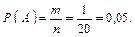
б) Элементарными исходами рассматриваемого эксперимента являются возможные варианты последовательного набора двух цифр из пяти. Так как в условии указано, что цифры нечетные, то выбирать будем две цифры из 1, 3, 5, 7, 9, с учетом того, что цифры могут повторяться.
Пространство элементарных исходов рассматриваемого эксперимента:
W = {(1, 1), (1, 3), (1, 5), (1, 7), (1, 9), (3, 1), (3, 3), (3, 5), (3, 7), (3, 9), (5, 1), (5, 3), (5, 5), (5, 7), (5, 9), (7, 1), (7, 3), (7, 5), (7, 7), (7, 9), (9, 1), (9, 3), (9, 5), (9, 7), (9, 9)}.
В данном случае пространство элементарных исходов состоит из 25 элементов: n = 25.
Поскольку цифры набираются случайным образом, все элементарные исходы равновозможны, и для вычисления вероятности интересующего нас события можно воспользоваться классическим методом определения вероятностей.
Событие B = {номер набран правильно с первой попытки}.
Число исходов, благоприятных событию В, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
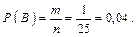
Ответ: а) вероятность того, что номер набран правильно с первой попытки, равна 0,05; б) вероятность того, что номер набран правильно с первой попытки, равна 0,04.
Задача 3 Предприятие объявляет конкурс на замещение 3 вакантных должностей. Из 10 человек, подавших свои документы на конкурс, – 6 женщин. Случайным образом отобраны 3 человека. Какая вероятность того, что среди отобранных окажутся:
а) все 3 женщины;
б) только одна женщина?
Решение. Обозначим события:
А = {из трех, случайным образом отобранных человек, – все три женщины};
В = {из трех, случайным образом отобранных человек, – одна женщина и двое мужчин}.
Найдем вероятности событий двумя способами:
1) пользуясь формулами комбинаторики;
2) пользуясь теоремами сложения и умножения вероятностей.
1а) Определим вероятность события А = {из трех, случайным образом отобранных человек, – все три женщины}.
Определим число способов выбора 3 человек из 10 – выборка неупорядоченная без возвращения.
Число способов определим по формуле
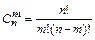 ,
, 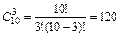 .
.
Определим число способов выбора 3 женщин из 6 женщин, подавших свои документы на конкурс: 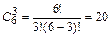 .
.
Вероятность события А Р (А) = 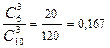 .
.
1б) Обозначим события:
А = {из трех, случайным образом отобранных человек, – все три женщины};
А 1 = {первый, случайным образом отобранный кандидат, – женщина}.
Р (А 1) = 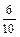 (всего 10 кандидатов, из них 6 женщин).
(всего 10 кандидатов, из них 6 женщин).
Событие А 2 = {второй, случайным образом отобранный кандидат, – женщина}.
Р (А 2 / А 1) = 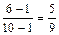 {всего осталось 9 кандидатов, из них 5 женщин}.
{всего осталось 9 кандидатов, из них 5 женщин}.
Событие А 3 = {третий, случайным образом отобранный кандидат, – женщина}.
Р (А3 / 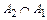 ) =
) = 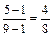 {всего осталось 8 кандидатов, из них 4 женщины}.
{всего осталось 8 кандидатов, из них 4 женщины}.
По теореме умножения вероятностей зависимых событий
P (А) = P (A 1) P (A 2/ А 1) P (А 3/ 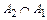 ) =
) = 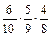 =
= 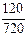 = 0,167.
= 0,167.
2а) В = {из трех, случайным образом отобранных человек – одна женщина и двое мужчин}.
Определим число способов выбора 3 человек из 10 по формуле
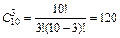 .
.
Определим число способов выбора одной женщины из 6 женщин, подавших свои документы на конкурс: 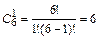 .
.
Определим число способов выбора двух мужчин из (10 – 6) = 4 мужчин, подавших свои документы на конкурс: 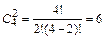 .
.
2б) Обозначим события:
В = {из трех, случайным образом отобранных человек, – одна женщина и двое мужчин};
С 1 = {первый, случайным образом отобранный кандидат, – женщина, второй – мужчина, третий – мужчина};
С 2 = {первый, случайным образом отобранный кандидат, – мужчина, второй – женщина, третий – мужчина};
С 3 = {первый, случайным образом отобранный кандидат, – мужчина, второй – мужчина, третий – женщина}.
По теореме сложения вероятностей несовместных событий
Р (В) = Р (С 1) + Р (С 2) + Р (С 3).
Вероятность события С 1 определим по формуле
Р (С 1) = P (В 1) P (В 2 / В 1) P (В 3/ 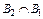 ).
).
Событие В 1 = {первый, случайным образом отобранный кандидат, – женщина}.
Вероятность события Р (В 1) = 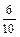 (всего 10 кандидатов, из них 6 женщин).
(всего 10 кандидатов, из них 6 женщин).
Событие В 2 = {второй, случайным образом отобранный кандидат, – мужчина}.
Вероятность события P (В 2 / В 1)= 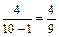 (всего осталось 9 кандидатов, из них 4 мужчин).
(всего осталось 9 кандидатов, из них 4 мужчин).
Событие В 3 = {третий, случайным образом отобранный кандидат, – мужчина, при условии, что первый и второй кандидаты (женщина и мужчина) уже отобраны}.
Вероятность события P (В 3 / 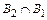 )=
)= 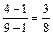 (всего осталось 8 кандидатов, из них 3 мужчин).
(всего осталось 8 кандидатов, из них 3 мужчин).
По теореме умножения вероятностей зависимых событий
P (С 1) = P (В 1) P (В 2 / В 1) P (В 3 / 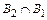 ) =
) = 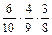 =
= 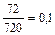 .
.
Вероятность события С 2 определим по формуле
Р (С 2) = P (В 1) P (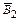 / В 1) P (В 3/
/ В 1) P (В 3/ 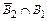 ).
).
Событие В 1 = {первый, случайным образом отобранный кандидат, – мужчина}.
Вероятность события Р (В 1) = 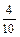 (всего 10 кандидатов, из них 4 мужчин).
(всего 10 кандидатов, из них 4 мужчин).
Событие 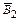 = {второй, случайным образом отобранный кандидат, – женщина}.
= {второй, случайным образом отобранный кандидат, – женщина}.
Вероятность события Р (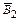 / В 1)=
/ В 1)= 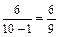 (всего осталось 9 кандидатов, из них 6 женщин).
(всего осталось 9 кандидатов, из них 6 женщин).
Событие В 3 = {третий, случайным образом отобранный кандидат, – мужчина}.
Вероятность события P (В3 / 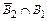 ) =
) = 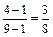 (всего осталось 8 кандидатов, из них 3 мужчин).
(всего осталось 8 кандидатов, из них 3 мужчин).
По теореме умножения вероятностей зависимых событий
P (С 2) = P (В 1) P (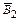 / В 1) P (В 3/
/ В 1) P (В 3/ 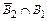 ) =
) = 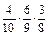 =
= 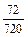 = 0,1.
= 0,1.
Вероятность события С 3 определим по формуле
Р (С 3)= P (В 1) P (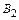 / В 1) P (
/ В 1) P (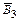 /
/ 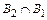 ).
).
Событие В 1 = {первый, случайным образом отобранный кандидат, – мужчина}.
Вероятность события Р (В 1) = 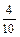 (всего 10 кандидатов, из них 4 мужчины).
(всего 10 кандидатов, из них 4 мужчины).
Событие В 2 = {второй, случайным образом отобранный кандидат, – мужчина}.
Вероятность события Р (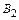 / В 1) =
/ В 1) = 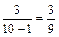 (всего осталось 9 кандидатов, из них 3 мужчин).
(всего осталось 9 кандидатов, из них 3 мужчин).
Событие В 3 = {третий, случайным образом отобранный кандидат, – женщина}.
Вероятность события Р (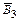 /
/ 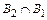 ) =
) = 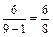 (всего осталось 8 кандидатов, из них 6 женщин).
(всего осталось 8 кандидатов, из них 6 женщин).
По теореме умножения вероятностей зависимых событий
P (С 3) = P (В 1) P (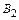 / В 1) P (
/ В 1) P (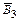 /
/ 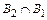 ) =
) = 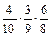 =
= 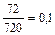 .
.
По теореме сложения вероятностей несовместных событий
Р (В) = Р (С 1) + Р (С 2) + Р (С 3) = 0,1+ 0,1+ 0,1 = 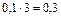 .
.
Ответ: а) вероятность того, что из трех, случайным образом отобранных человек, – все три женщины, равна 0,167;
б) вероятность того, что из трех, случайным образом отобранных человек, – одна женщина и двое мужчин, равна 0,3.
Задача 4 Два клиента зашли в магазин. Вероятность того, что первый клиент пожелает сделать покупку, равна 0,7, для второго клиента эта вероятность равна 0,5. Найти вероятность того, что захотят сделать покупку:
а) оба клиента;
б) только один клиент;
в) хотя бы один клиент.
Решение. Обозначим события:
Ai = { i -й клиент пожелает сделать покупку}, i = 1, 2;
B = {оба клиента пожелают сделать покупку};
C = {только один клиент из двух пожелает сделать покупку};
D = {хотя бы один клиент из двух пожелает сделать покупку}.
Согласно условию, вероятность события A 1 P (A 1) = 0,7, вероятность события A 2 P (A 2) = 0,5.
Тогда вероятности противоположных событий: 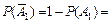
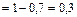 ,
, 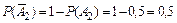 .
.
Определим все элементарные события данного случайного эксперимента и соответствующие вероятности:
| Элементарное событие | Событие | Вероятность |
 | 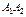 | 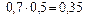 |
 | 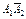 | 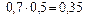 |
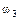 | 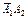 | 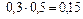 |
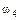 | 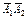 | 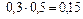 |
| Итого | 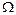 |
Событие B можно представить в виде 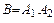 .
.
Полагая, что события Ai (i = 1, 2) – независимы, и применяя теорему умножения вероятностей независимых событий, получим
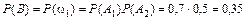 .
.
Событие С можно представить в виде 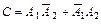 .
.
Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
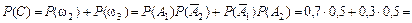
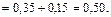
Событие D можно представить в виде 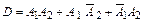 или в виде
или в виде  =
= 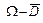 ,
,
где  – событие, противоположное событию
– событие, противоположное событию  :
:  = {оба клиента не пожелают сделать покупку}.
= {оба клиента не пожелают сделать покупку}.
Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим

 ,
,
или  , где
, где 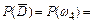
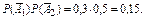
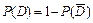 = 1 – 0,15 = 0,85.
= 1 – 0,15 = 0,85.
Ответ: а) вероятность того, что захотят сделать покупку оба клиента, равна 0,35; вероятность того, что покупку пожелает сделать только один клиент из двух, равна 0,50; вероятность того, что покупку пожелает сделать хотя бы один клиент, равна 0,85.
Задача 5 Сотрудники отдела маркетинга полагают, что в ближайшее время ожидается рост спроса на продукцию фирмы. Вероятность этого они оценивают в 30 %. При росте спроса на продукцию, вероятность расширения фирмы в ближайшее время составит 0,4, если спрос на продукцию не возрастет, то вероятность расширения фирмы составит 0,2. Определить вероятность расширения фирмы в ближайшее время. Фирма расширилась, какова вероятность того, что спрос на продукцию возрос?
Решение. 1 Определим событие A = {в ближайшее время произойдет расширение фирмы}.
2 Относительно условий рассматриваемого случайного эксперимента, состоящего в том, что в ближайшее время произойдет расширение фирмы, можно выдвинуть две несовместные гипотезы:
H 1 = {спрос на продукцию фирмы возрастет};
H 2 = {спрос на продукцию фирмы не возрастет}.
Причём H 1 + H 2 = W.
Учитывая свойство вероятностей гипотез P (H 1) + P (H 2) = 1, определим:
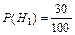 = 0,3;
= 0,3; 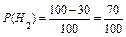 = 0,7.
= 0,7.
3 Условные вероятности события A = {в ближайшее время произойдет расширение фирмы} при осуществлении этих гипотез известны и равны:
P (A | H 1) = 0,4; P (A | H 2) = 0,2.
Для определения вероятности события A воспользуемся формулой полной вероятности
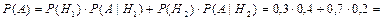
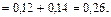
Для определения вероятности того, что спрос на продукцию возрос при условии, что фирма расширилась, воспользуемся формулой Байеса
 ,
,

Ответ: вероятность того, что в ближайшее время произошло расширение фирмы, равна 0,26; вероятность того, что спрос на продукцию возрос при условии, что фирма расширилась, равна 0,462.
Задача 6 В городе 8 коммерческих банков, работающих независимо друг от друга. У каждого банка риск банкротства в течение года составляет 5 %. Определить вероятность того, что в течение года обанкротится:
а) один коммерческий банк;
б) хотя бы один коммерческий банк;
в) не менее двух коммерческих банков.
Решение. Условие задачи можно рассматривать как серию из n = 8 независимых испытаний, в каждом из которых вероятность наступления события A = {коммерческий банк обанкротится в течение года} одинакова и равна:
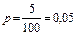 ; q = 1 – p = 1 – 0,05 = 0,95.
; q = 1 – p = 1 – 0,05 = 0,95.
а) Для вычисления вероятности события B = {в течение года обанкротится один коммерческий банк из восьми} воспользуемся формулой Бернулли
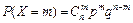 , где 0 £ p £ 1; q = 1 – p; m = 0, 1, 2,…, n.
, где 0 £ p £ 1; q = 1 – p; m = 0, 1, 2,…, n.
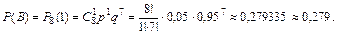
б) При вычислении вероятности события C = {в течение года обанкротится хотя бы один коммерческий банк из восьми} удобно перейти к рассмотрению события 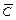 = {в течение года не обанкротится ни один коммерческий банк}:
= {в течение года не обанкротится ни один коммерческий банк}:
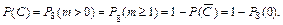
Применяя формулу Бернулли, вычисляем:


в) При вычислении вероятности события D = {в течение года обанкротится не менее двух коммерческих банков} удобно перейти к рассмотрению события 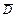 = {в течение года обанкротится менее двух коммерческих банков}:
= {в течение года обанкротится менее двух коммерческих банков}:

Применяя формулу Бернулли, вычисляем:
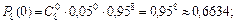

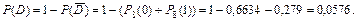
Ответ: вероятность того, что в течение года обанкротится:
а) один коммерческий банк, равна 0,279;
б) хотя бы один коммерческий банк, равна 0,3366;
в) не менее двух коммерческих банков, равна 0,0576.
Задача 7 Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по 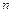 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие, составляет
адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие, составляет  %. Определить:
%. Определить:
а) какова вероятность того, что из 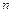 разосланных анкет «возвратятся» не более
разосланных анкет «возвратятся» не более  анкет;
анкет;
б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие, и соответствующую этому значению вероятность.
Рассмотрим решение задачи для двух вариантов:
| Вариант | n | p, % | k |
| Первый | |||
| Второй |
Решение. Первый вариант.
а) Условие задачи можно рассматривать как серию из n = 100 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью 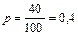 может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6.
может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6.
Определим наиболее вероятное число анкет, «возвратившихся» на предприятие по формуле
np – q £ m 0 £ np + p.
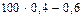 £ m 0 £
£ m 0 £ 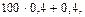
39,4 £ m 0 £ 40,4.
Наивероятнейшее число m 0 = 40.
Так как число испытаний достаточно велико для вычисления вероятностей событий B = {из 100 разосланных анкет менее 40 «возвратились» на предприятие} и C = {из 100 разосланных анкет ровно 40 «возвратились» на предприятие } можно воспользоваться приближёнными формулами Муавра-Лапласа:
1) Для вычисления вероятности события B воспользуемся интегральной теоремой Муавра-Лапласа при n = 100; p = 0,4; q = 1 – 0,4 = 0,6; k 1 = 0; k 2 = 40:
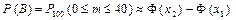 ;
;

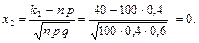
По таблицам значений функции 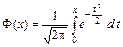 находим F (–8,165) = = – 0,5, F (0) = 0,0.
находим F (–8,165) = = – 0,5, F (0) = 0,0.
Таким образом,
 .
.
2) Для вычисления вероятности события С воспользуемся локальной теоремой Муавра-Лапласа. В данном случае n = 100; p = 0,4; q = 0,6; m = 40:


По таблицам значений функции 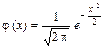 находим j (0) = 0,3989.
находим j (0) = 0,3989.
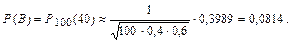
Ответ: а) вероятность того, что из 100 разосланных анкет не более 40 «возвратятся» на предприятие, равна 0,5; б) наиболее вероятное число разосланных анкет, «возвратившихся» на предприятие, составит 40, соответствующая этому числу вероятность 0,0814.
Решение. Второй вариант.
б) Условие задачи можно рассматривать как серию из n = 200 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью 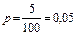 может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,05 = 0,95.
может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,05 = 0,95.
Определим наиболее вероятное число анкет, «возвратившихся» на предприятие, по формуле
np – q £ m 0 £ np + p,
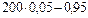 £ m 0 £
£ m 0 £ 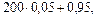
9,05 £ m 0 £ 10,05.
Наивероятнейшее число m 0 = 10.
В данном случае для вычисления вероятностей воспользуемся приближенной формулой Пуассона с параметром a = np, так какчисло испытаний n = 200достаточно велико, а вероятность появления события в каждом испытании p = 0,05очень мала (p < 0,1), то есть в каждом отдельном опыте событие A появляется крайне редко:

Таблица значений функции  приведена в приложении В.
приведена в приложении В.
a = np =  .
.
1) Определим событие В = {не более двух анкет «возвратятся» на предприятие, то есть или 0, или 1, или 2}.

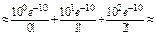
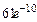 = 0,0028.
= 0,0028.
2) Определим событие С = {10 анкет «возвратятся» на предприятие}.
Вероятность события С
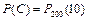
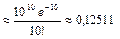 .
.
Ответ: а) вероятность того, что из 200 разосланных анкет не более 2 «возвратятся» на предприятие, равна 0,002769; б) наиболее вероятное число разосланных анкет, «возвратившихся» на предприятие, составит 10, соответствующая этому числу вероятность 0,12511.
Задача 8а Для определённой в условии задачи дискретной случайной величины:
а) построить ряд распределения и столбцовую диаграмму;
б) найти функцию распределения и построить её график;
в) вычислить числовые характеристики: математическое ожидание, моду, дисперсию и среднее квадратичное отклонение.
Студент пришел на экзамен, зная ответы на 3/4 вопросов по каждому из трёх разделов программы. Случайная величина X – число вопросов, на которые он сможет ответить при условии, что экзаменационный билет содержит по одному вопросу из каждого раздела.
Решение. а) Возможные значения данной случайной величины X: 0, 1, 2, 3. Условие задачи можно рассматривать как серию из n = 3 независимых испытаний, в каждом из которых вероятность события A = {студент сумеет ответить на поставленный вопрос} равна 3/4. В данном случае для вычисления вероятностей возможных значений случайной величины X воспользуемся формулой Бернулли:
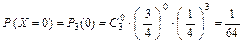 ;
;
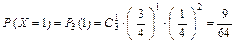 ;
;
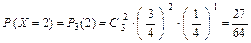 ;
;
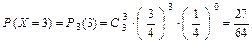 .
.
(Проверим, что 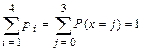 .)
.)
Ряд распределения данной случайной величины X:
| xi | Итого | ||||
| pi | 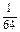 | 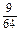 | 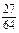 | 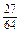 | |
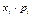 | 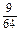 | 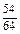 | 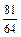 | 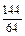 | |
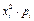 | 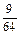 | 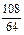 | 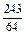 | 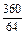 |
Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 28.
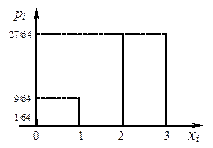
Рисунок 28 – Столбцовая диаграмма
б) Вычислим функцию распределения данной случайной величины:
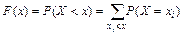 :
:
при x Î (- ¥, 0] 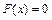 ;
;
при x Î (0, 1] 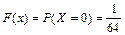 ;
;
при x Î (1, 2] 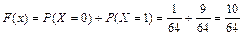 ;
;
при x Î (2, 3] 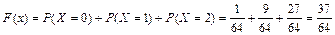 ;
;
при x Î (3, +¥) 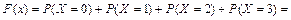
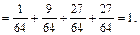
Итак, функция распределения рассматриваемой случайной величины
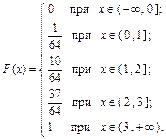
График функции F (x) приведён на рисунке 29.
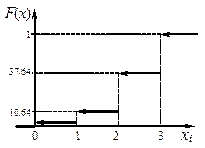
Рисунок 29 – Функция распределения
в) Вычислим числовые характеристики данной случайной величины.
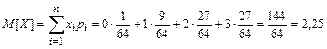 [вопросов],
[вопросов],
то есть среднее число вопросов, на которые студент сможет дать ответ, равно 2,25.
Как следует из ряда распределения, данная случайная величина имеет две моды: 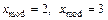 , то есть наиболее вероятное число вопросов, на которые студент сможет дать ответ, равно 2 и 3.
, то есть наиболее вероятное число вопросов, на которые студент сможет дать ответ, равно 2 и 3.
Дисперсия
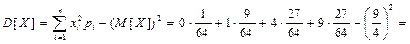
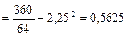 [вопросов2].
[вопросов2].
Среднее квадратическое отклонение 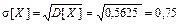 [вопросов], то есть среднее квадратическое отклонение числа вопросов, на которые студент сможет дать ответ, равно 0,75.
[вопросов], то есть среднее квадратическое отклонение числа вопросов, на которые студент сможет дать ответ, равно 0,75.
Задача 8б Три клиента зашли в магазин. Вероятности совершения покупки для каждого из трех клиентов соответственно равны: 0,7; 0,6; 0,8. Случайная величина X – число клиентов, которые совершат покупку в магазине.
Решение.а) Возможные значения данной случайной величины X: 0, 1, 2, 3. Условие задачи можно рассматривать как серию из n = 3 независимых испытаний. В данном случае для вычисления вероятностей возможных значений случайной величины X можно воспользоваться теоремами сложения вероятностей несовместных событий и умножения вероятностей независимых событий:
Обозначим события:
A i = { i -й клиент совершит покупку}, i = 1, 2, 3.
Согласно условию вероятность события A 1 P (A 1) = 0,7, вероятность события A 2 P (A 2) = 0,6, вероятность события A 3 P (A 3) = 0,8. Тогда вероятности противоположных событий: 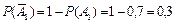 ,
, 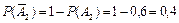 ,
, 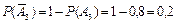 .
.
Определим все элементарные события данного случайного эксперимента и соответствующие вероятности:
| События | Элементарные события | Вероятности |
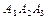 | 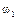 | 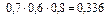 |
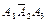 | 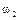 | 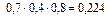 |
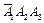 | 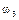 | 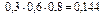 |
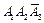 | 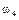 | 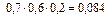 |
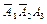 | 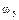 | 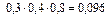 |
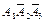 | 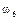 | 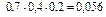 |
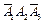 |  | 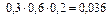 |
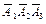 | 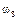 |  |
| Итого | 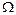 |


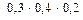 = 0,024;
= 0,024;
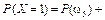
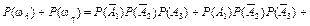
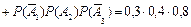 +
+ 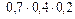 +
+ 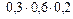 = 0,096 + + 0,056 + 0,036 = 0,188;
= 0,096 + + 0,056 + 0,036 = 0,188;
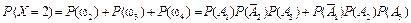
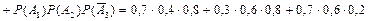 = 0,224 + + 0,144 +0,084 = 0,452;
= 0,224 + + 0,144 +0,084 = 0,452;
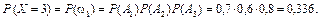
(Проверим, что 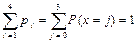 ).
).
Ряд распределения данной случайной величины X:
| xi | Итого | ||||
| pi | 0,024 | 0,188 | 0,452 | 0,336 | |
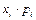 | 0,188 | 0,904 | 1,008 | 2,1 | |
 | 0,188 | 1,808 | 3,024 | 5,02 |
Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 30.

Рисунок 30 – Столбцовая диаграмма
б) Вычислим функцию распределения данной случайной величины:
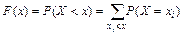 :
:
при x Î (- ¥, 0] 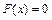 ;
;
при x Î (0, 1] 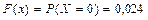 ;
;
при x Î (1, 2] 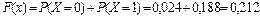 ;
;
при x Î (2, 3] 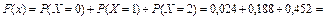
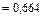 ;
;
при x Î (3, +¥) 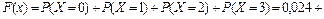
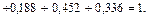
Итак, функция распределения рассматриваемой случайной величины
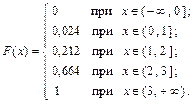
График функции F (x) приведён на рисунке 31.
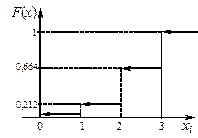
Рисунок 31 – Функция распределения
в) Вычислим числовые характеристики данной случайной величины.
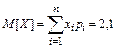 [клиентов], то есть среднее число клиентов, которые совершат покупку в магазине, равно 2,1.
[клиентов], то есть среднее число клиентов, которые совершат покупку в магазине, равно 2,1.
Как следует из ряда распределения, данная случайная величина имеет моду 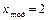 [клиентов], (для xi = 2 вероятность принимает максимальное значение pi = 0,452), то есть наиболее вероятное число клиентов, которые совершат покупку в магазине, равно 2.
[клиентов], (для xi = 2 вероятность принимает максимальное значение pi = 0,452), то есть наиболее вероятное число клиентов, которые совершат покупку в магазине, равно 2.
Дисперсия 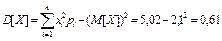 [клиентов 2 ].
[клиентов 2 ].
Среднее квадратическое отклонение 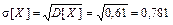 [клиентов], то есть среднее квадратическое отклонение числа клиентов, которые совершат покупку в магазине, равно 0,671.
[клиентов], то есть среднее квадратическое отклонение числа клиентов, которые совершат покупку в магазине, равно 0,671.
Задача 9 Закон распределения непрерывной случайной величины задан функцией плотности распределения вероятностей f (x). Требуется:
а) определить значение параметра c;
б) построить график функции плотности распределения вероятностей;
в) найти функцию распределения данной случайной величины и построить её график;
г) вычислить числовые характеристики данной случайной величины: математическое ожидание, моду, медиану, дисперсию, среднее квадратичное отклонение;
д) найти вероятность того, что данная случайная величина примет значение, принадлежащее отрезку [ a; b ]:
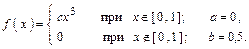
Решение. а) Для определения неизвестного параметра c воспользуемся соотношением
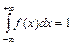 .
.
В данном случае имеем
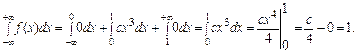
Отсюда 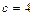 .
.
Таким образом, функция плотности распределения вероятностей
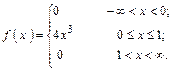
б) График функции f (x) изображён на рисунке 32.
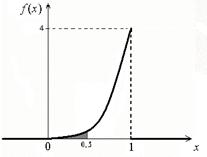
Рисунок 32 – График плотности распределения f (x)
в) Вычислим функцию распределения данной случайной величины:
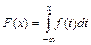 ,
,
при x Î (- ¥, 0] 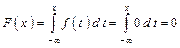 ;
;
при x Î (0, 1] 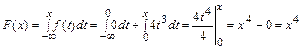 ;
;
при x Î (1, + ¥) 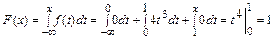 .
.
Итак, 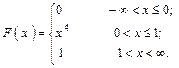
График функции F (x) приведён на рисунке 33.
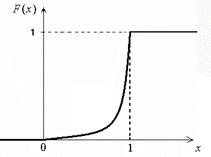
Рисунок 33 – График функции распределения F (x)
г) Вычислим числовые характеристики данной случайной величины.
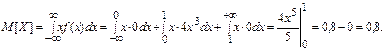
Для вычисления дисперсии воспользуемся формулой

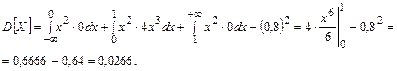
Среднее квадратическое отклонение 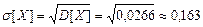 .
.
Мода данной случайной величины, как следует из графика функции f (x), равна 1.
Для определения медианы воспользуемся соотношением
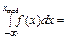
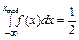 ,
,
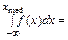
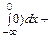
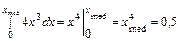 ,
,
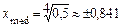 .
.
По условию плотность распределения случайной величины не равна 0 в интервале 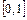 , поэтому
, поэтому 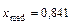 .
.
Медиану также можно определить из соотношения F (x med) = 0,5.
Решая уравнение 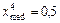 , получим
, получим 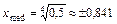 .
.
По условию плотность распределения случайной величины равна 0 в интервале 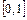 , поэтому
, поэтому 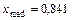 .
.
д) Для вычисления вероятности того, что случайная величина Х примет значение, принадлежащее отрезку [0; 0,5], можно воспользоваться, например, соотношением 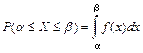 ,
,
 2015-01-07
2015-01-07 11151
11151

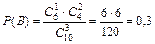 .
.