Говорят, что дискретная случайная величина X распределена по закону Пуассона, если ее возможные значения: 0, 1, 2, …, m,… (счетное множество значений), а соответствующие им вероятности задаются формулой
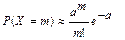 (26)
(26)
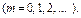
Таблица значений вероятности для различных значений 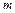 и
и 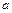 приведена в приложении В.
приведена в приложении В.
Таким образом, ряд распределения случайной величины X, распределенной по закону Пуассона, имеет вид:
| xi | … | k | … | |||
| pi | e – a | ae – a | (a 2 e – a )/2! | … | (ake – a )/ k! | … |
Закон распределения Пуассона зависит от одного параметра: a. Доказано, что для случайной величины, распределенной по закону Пуассона,
M [ X ] = a, D [ X ] = a, 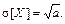
Рассмотрим условия, при которых возникает распределение Пуассона.
1 Распределение Пуассона с параметром a = np можно приближенно применять вместо биномиального распределения, когда число испытаний n достаточно велико, а вероятность появления события в каждом испытании p очень мала (p < 0,1), то есть в каждом отдельном опыте событие A появляется крайне редко. Отсюда происходит использующееся еще иногда для закона Пуассона название «закон редких событий».
2 По закону Пуассона распределена случайная величина, описывающая число событий простейшего потока, произошедших в течение промежутка времени t.
Простейший поток событий. Потоком событий называется последовательность однородных событий, наступающих одно за другим в случайные моменты времени.
Интенсивностью потока l называется среднее число событий, происходящих за единицу времени.
Если l = const, то поток называется стационарным. Это свойство означает, что вероятность наступления того или иного числа событий в течение отрезка времени длиной t не зависит от расположения на оси времени этого отрезка, а зависит только от его длины.
Поток называется ординарным, если вероятность попадания на малый участок D t двух и более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события. Грубо говоря, это означает, что события возникают поодиночке, а не группами по два, по три и т. д.
Поток событий называется потоком без последействия, если вероятность попадания того или иного числа событий на какой-то отрезок времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним участок, то есть предыстория потока не сказывается на вероятности появления событий в ближайшем будущем. Эта независимость физически сводится к тому, что события появляются на оси времени в силу случайных причин, индивидуальных для каждого из них.
Поток, обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим.
Доказано, что для простейшего потока число событий, попадающих на каждый отрезок времени длиной t, распределено по закону Пуассона с параметром a = l t, где l – интенсивность потока.
Пример 34 Коммутатор учреждения обеспечивает соединение 400 абонентов по внутренней связи, для каждого из которых вероятность того, что он позвонит на коммутатор в течение часа, равна 0,01. Найти вероятность того, что в течение часа: а) 5 абонентов позвонят на коммутатор; б) не более 4 абонентов позвонят на коммутатор; в) более 4 абонентов позвонят на коммутатор.
Решение. Случайная величина X, определяющая число абонентов, позвонивших на коммутатор в течение часа, может принимать значения 0, 1, 2, …, 400. Определим событие В = {в течение часа 5 абонентов позвонят на коммутатор}.
Так как число испытаний велико, а вероятность наступления события A = {в течение часа абонент позвонит на коммутатор} очень мала (p = 0,01 < 0,1), то в этом случае можно воспользоваться приближенной формулой Пуассона
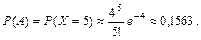
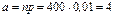 .
.
Определим событие С = {в течение часа не более 4 абонентов позвонят на коммутатор, то есть или 0, или 1, или 2, или 3, или 4}.
Воспользуемся приближенной формулой Пуассона и теоремой сложения вероятностей несовместных событий:
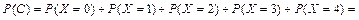
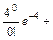
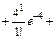
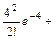
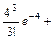
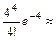 0,0183 + 0,0733 + 0,1465 + 0,1954 +
0,0183 + 0,0733 + 0,1465 + 0,1954 +
+ 0,1954 = 0,6289.
Определим событие D ={в течение часа более 4 абонентов позвонят на коммутатор, то есть или 5, или 6, или 7, или 8, …}.
События С и D – противоположные, то есть С + D= 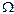 ,Р (С)+ Р (D) = 1,
,Р (С)+ Р (D) = 1,
Р (D)= 1 – Р (С)= 1 – 0,6289 = 0,3711.
Пример 35 К абоненту АТС в среднем поступает 1,5 вызова в час. Поток вызовов можно считать простейшим. Для этого промежутка времени найти вероятность того, что: а) в течение часа поступит хотя бы один вызов; б) в течение трех часов произойдет не менее четырех вызовов.
Решение. а) Случайная величина X 1, определяющая число вызовов, поступивших в течение часа, может принимать значения 0, 1, 2, 3,… и, согласно условию, распределена по закону Пуассона с параметром a = l t = 1,5 (так как интенсивность потока l = 1,5; t = 1[ час ]). Обозначим событие: A= {в течение часа поступит хотя бы один вызов}. Тогда
P (A) = P (X 1 ³ 1) = 1 – P (X 1 = 0) = 1 – (a 0 e – a )/0! = 1 – е –1,5 = 1 – 0,22313 =0,77687.
б) Для определения вероятности события B = {в течение трех часов поступит не менее четырех вызовов} введем в рассмотрение случайную величину X 2, определяющую число вызовов, поступивших в течение трех часов. Эта случайная величина распределена по закону Пуассона с параметром a = l t = 1,5 × 3 = 4,5:
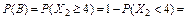
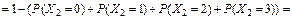
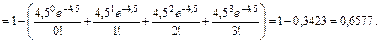
 2015-01-07
2015-01-07 2068
2068
