Метод Ньютона (касательных)

Пусть x ₀ – начальное приближение к корню, а f (x) имеет непрерывную производную. Следующее приближение к корню найдем в точке x ₁, где касательная к функции f (x), проведенная из точки (x ₀, f ₀), пересекает ось абсцисс. Затем точно так же обрабатываем точку (x ₁, f ₁), организуя итерационный процесс. Выход из итерационного процесса по условию .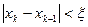

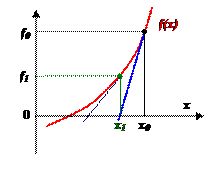Уравнение касательной, проведенной из точки (x ₀, f ₀): y (x) = f ^/(x ₀)(x – x ₀) + f (x ₀) дает для y (x ₁) = 0 следующее выражение:

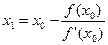, (1)

которое и используется для организации итерационного процесса. Итерации сходятся, только если всюду выполняется условие 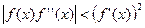; в противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня. Итерации будут сходиться к корню с той стороны, с которой .

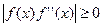Метод обладает самой высокой скоростью сходимости: погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Метод можно использовать для уточнения корней в области комплексных чисел, что необходимо при решении многих прикладных задач, например при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии.

Недостатком метода можно указать необходимость знать явный вид первой и второй производных, так как их численный расчет приведет к уменьшению скорости сходимости метода. Иногда, ради упрощения расчетов, используют т.н. модифицированный метод Ньютона, в котором значение f ^/(x) вычисляется только в точке x ₀, при этом число итераций увеличивается, но расчеты на каждой итерации упрощаются.