2015-01-07
320
Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение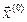 
, а исходная система уравнений преобразуется к эквивалентной системе вида
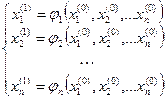, (5)
и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим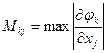 
. Достаточным условием сходимости является 
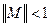. Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций 
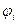, которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.
Например, для исходной системы уравнений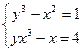 
эквивалентная итерационная система (5) может быть представлена в следующем виде:
,
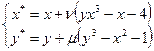где множители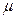 
= –0.15и 
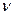= –0.1 подбираются из анализа условий сходимости.
