Внешнее гравитационное поле Земли по данным искусственных спутников Земли

До запуска спутников внешнее гравитационное поле Земли описывалось простой двучленной формулой (см.(2)):

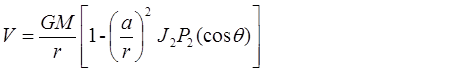
Было бы неправильным думать, что гравитационное поле нашей планеты столь просто. В действительности простота гравитационного поля Земли была связана с тем, что не удавалось покрыть Землю детальной сетью гравиметрической съемки, которая позволила бы выявить другие поправки к основной, ньютоновской части поля (см. (1)):

В общем случае гравитационный потенциал любого гравитирующего космического тела – планеты, спутника или звезды – может быть разложен по сферическим функциям. Поместив начало координат в центр масс Земли и совместив оси координат с главными осями инерции планеты, по данным ИСЗ получили разложение гравитационного потенциала Земли в следующем простом виде:

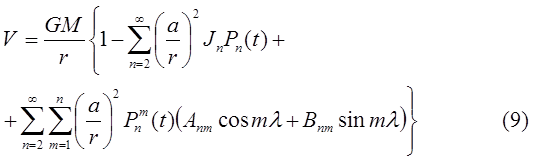
Здесь r, θ, λ – сферические координаты в точке наблюдений, t=cos θ, P_n – полином Лежандра n -го порядка (он представляет полином n -го порядка относительно cos θ), 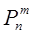- присоединенные полиномы Лежандра – полиномы n -го порядка относительно cos θ и sin θ. 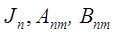- гравитационные моменты, определяемые экспериментально по траекториям искусственных спутников.

До запуска спутников в разложении (9) был определен всего лишь один коэффициент J₂, причем это потребовало проведения огромного количества геодезических и гравиметрических съемок по всей Земле. Широкое использование искусственных спутников для геодезических целей радикально изменило положение. Уже к началу 60-х годов позволило определить примерно 10 зональных моментов J_n и несколько десятков тессеральных моментов A_nm и B_nm. Зональные моменты J_n в разложении потенциала (9) вызывают вековые возмущения орбит ИСЗ. Поэтому для их определения используются сравнительно длинные ряды наблюдений, и они определены точнее, чем тессеральные моменты A_nm и B_nm, которые вызывают только короткопериодические изменения элементов орбит.