Динамической системой называется математическая модель в совокупности взаимосвязанных элементов, удовлетворяющая следующим аксиомам:
1. Заданы множество моментов времени Т, множество состояний X, множество мгновенных значений U, множество их допустимых значений Ω={ω; T→U}, множество мгновенных значений выходов Y и множество их допустимых значений Г = {n: Т*Х→Y}
Существует переходная функция состояний
Ф= {φ: T*T*X*Ω→X}
Значениями которой являются состояния системы в которых она оказывается в момент времени t, если в момент времени t0 она была в состоянии х0 и на нее воздействовал вход ω
x(t) = φ [ t; t0; x(t0); ω ] 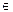 X
X
φ обладает следующими свойствами:
1) свойство направленности, то есть φ - определена для всех t 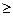 t0 и не обязательно определена для t < t0
t0 и не обязательно определена для t < t0
2) φ согласована со своими начальными значениями, т. е.
x(t0) = [t0, x(t0), ω], t 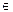 T, x
T, x 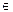 X, ω
X, ω 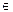 Ω
Ω
3) для всех отрезков входных воздействий ω1, ω2… 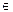 Ω таких, что ω1=ω2 для всех t0 < t
Ω таких, что ω1=ω2 для всех t0 < t 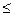 t1 имеет место равенство
t1 имеет место равенство
φ [t1; t0; x(t0); ω1] = φ [t1; t0; x(t0); ω2]
это свойство управляемости.
4) φ обладает полугрупповым свойствам:
φ [t3; t1; x(t1); ω] = φ [t3; t2; φ [t2; t1; x(t1); ω] ω]
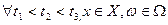
5) задано выходное отображение
Г = {η: Т*Т→Y}, которое определяет выход системы
y(t) = η [ t, x(t) ]
Цель ее определение
Цель – (искомое решение проблемы) – есть субъективный образ (абстрактная модель) несуществующего но желаемого состояния среды, которое решало бы возникшую проблему.
В этом смысле «системе» есть средство достижения цели.
Пусть дана некоторая система, которая определена следующим образом:
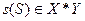
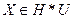
Тогда цель для системы 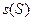 определяется следующей совокупностью:
определяется следующей совокупностью:
1) целевой функцией (функцией выполнения) G;
а) целевая функция определяется следующим образом: 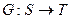 . Целевая функция в общем случае является некоторым функционалом.
. Целевая функция в общем случае является некоторым функционалом.
2) Т – функцией допустимости 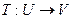 ;
;
3) Множество значений мер выполнения V;
4) Мерой выполнения может быть некоторая достижимая ошибка, ограничение на точность и так далее.
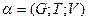 - цель;
- цель;
5) Проблема решения:
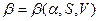 .
.
Изоморфные и гомоморфные системы
Для того чтобы система была системой, определяемой состоянием, необходимо и достаточно, чтобы ее можно было представить в виде канонической модели. Каноническое представление приводит к системе адекватной исходной с точностью до изоморфизма.
Определение 1. Каноническое представление двух систем изоморфно, если взаимооднозначное преобразование одной из них в состояние другой может превратить одно представление в другое.
Пример: 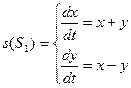
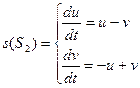
Если осуществим замену 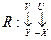 , то системы будут изоморфны, т.е. их нельзя будет отличить.
, то системы будут изоморфны, т.е. их нельзя будет отличить.
Гомоморфизм – одностороннее преобразование.
Это преобразование, приложенное к более сложной системе, может свести
ее к форме изоморфной более простой системы.
Пример. Задана система 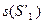 Система
Система 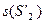
| a | b | c | d | e | |
| i | b | a | b | c | a |
| j | a | b | c | b | c |
| k | a | b | b | e | d |
| e | b | c | a | e | e |
| g | h | |
| α | g | h |
| β | h | h |
Преобразуем систему 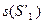 посредством однозначного лишь в одну сторону преобразования T
посредством однозначного лишь в одну сторону преобразования T
| a | b | c | d | e | i | j | k | l |
| h | h | h | g | g | β | β | α | α |
Преобразование Т однозначное, но не взаимно однозначное.
| ↓ | h | h | h | g | g |
| β | h | h | h | h | h |
| β | h | h | h | h | h |
| α | h | h | h | g | g |
| α | h | h | h | g | g |
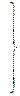
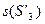
С точностью до обозначений выделяется в 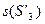 система соответствующая системе
система соответствующая системе 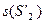 . Можно записать:
. Можно записать: 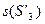 изоморфна
изоморфна 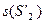 . Таким образом система
. Таким образом система 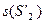 эквивалентна упрощенному образу системы
эквивалентна упрощенному образу системы 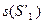 .
.
Определение 2. Две системы гомоморфные, если они становятся
одинаковыми при упрощении одной из них.
Определение 3. Если две системы находятся в таком отношении + друг к другу, что некоторое однозначное лишь в одну сторону преобразование, приложенное к одной из них, дает новую систему, изоморфную другой, то эта новая система (более простоя) есть гомоморфный образ первой системы.
 2014-09-02
2014-09-02 742
742








