Решение произвольных систем линейных уравнений. Метод Жордана-Гаусса. Теорема Кронекера – Капелли

Пусть дана произвольная система m линейных уравнений с n неизвестными:

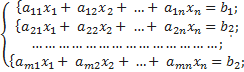
Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера-Капелли:

Система линейных алгебраических уравнений совместна

тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Правило решения произвольной сист. линейных уравнений:

Найти ранги основной и расширенной матриц системы. Если

r(A) ≠ r(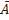) то система несовместна.

Если r(А) = r(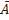) = r, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы,называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения

отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные n - r неизвестных называют свободными и переносят в правые части уравнений.

Найти выражения главных неизвестных через свободные. Получено общее решение системы.

Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частн. решения исходной сист. уравнений.

Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.

Пусть дана система уравнений:

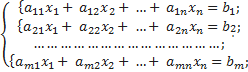
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (В частности, треугольному) виду.На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

7.Однородные системы линейных уравнений.

Аналитическая геометрия

Для того, чтобы система однородных уравнений имела

ненулевые решения, необходимо и достаточно, чтобы ранг r ее основ­

ной матрицы был меньше числа n неизвестных, Т. е. r < n.

Для того, чтобы однородная система n линейных урав­

нений с n неизвестными имела ненулевые решения, необходимо и до­

статочно, чтобы ее определитель 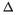был равен нулю, т. е. 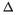= 0.

Если система имеет ненулевые решения, то 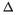= О. Ибо при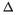 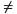0

система имеет только единственное(, нулевое решение. Если же 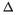= О,

то ранг r основной матрицы системы меньше числа неизвестных, т. е.

r < n. И, значит, система имеет бесконечное множество (ненулевых)

решений.