2015-01-13
4586
Смешанное произведение не меняется при циклической перестановке его сомножителей (не меняется ни объем параллелепипеда, ни ориентация его ребер):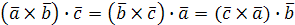 
.
Смешанное произведение не меняется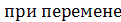 
знаков векторного и скалярного умножения: 
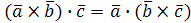, поэтому смешанное произведение записывают 
.
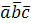Смешанное произведение меняет свой знак при перемене любых двух вектор-сомножителей: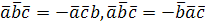 
, 
.
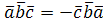Смешанное произведение ненулевых векторов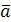 
, 
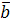и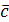 
равно нулю тогда и только тогда, когда они компланарны: 
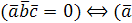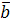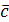, , – компланарны 
.
Доказательство. Предположим, что векторы 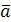, 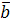и 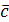– не компланарны. Тогда можно построить параллелепипед имеющий объем 
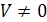, т.е. 
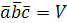, но это противоречит условию, согласно которого, 
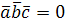. Следовательно, векторы 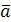, 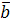и 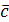– компланарны.
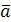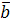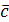Обратно, пусть , и – компланарны. Тогда вектор 
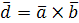и перпендикулярен плоскости, в которой находятся векторы 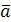, 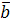и 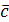, значит, он перпендикулярен любому вектору, лежащему в этой плоскости, например 
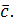Это значит, что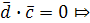 
.
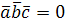Приложения смешанного произведения:
Определение взаимной ориентации векторов в пространстве.
Есл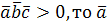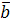и 
, и 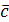– правая тройка, если 
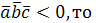левая.
Установление компланарности векторов:
(
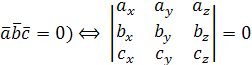Þ (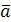, , 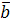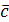– компланарны).
Определение объема параллелепипеда и треугольной пирамиды (тетраэдра):
, 
.
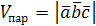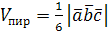Пример. Компланарны ли векторы 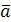, 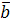и 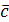, если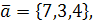 
.
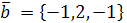
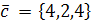Решение. Вычислим смешанное произведение векторов:
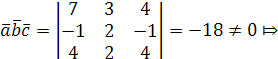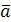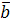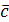векторы , и не компланарны.
