2015-01-13
3820
Теорема Ферма.
Если функция у = f (х), определенная в интервале (а; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
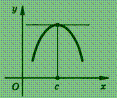
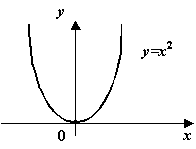
Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).
Найти наибольшее и наименьшее значение функции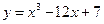 
на отрезке 
.
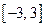Решение.
Найдем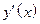 
, и точки, где 
.
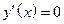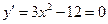, если 
.
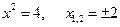Обе точки принадлежат рассматриваемому интервалу.
Найдем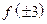 
и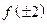 
и сравним полученные результаты.
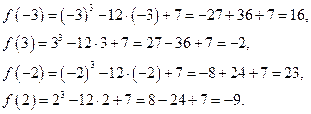
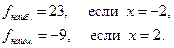
Пример 5.1 Функция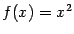 
имеет на отрезке 
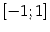точку минимума 
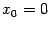. Производная функции существует при всех 
: 
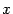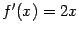. В точке минимума производная, действительно, оказывается равной 0: 
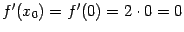, так что утверждение теоремы Ферма выполнено.
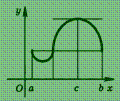
Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [ а; b ] и дифференцируемая в интервале (а; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а; b) существует такая точка с, что f ′(с) = 0.
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).
Пример 1. Докажем, что между двумя нулями дифференцируемой функции лежит, по крайней мере, один нуль ее производной.
