2015-01-13
1071
Механическая волна −процесс распространения колебаний в упругой среде.
Волновая поверхность −геометрическое место точек, совершающих колебания в одной фазе.
Плоская волна −волна, волновые поверхности которой представляют параллельные плоскости.
Уравнение плоской волны, распространяющейся в положительном направлении оси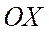 
:
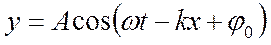, где 
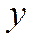− смещение точки среды из положения равновесия; 
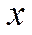− координата точки среды, колебания которой рассматриваются; 
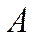− амплитуда волны; 
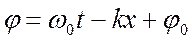− фаза волны; 
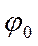− фаза колебаний в начальный момент времени; 
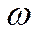− циклическая частота волны; 
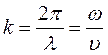− волновое число; 
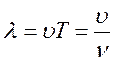− длина волны; 
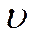− фазовая скорость волны; 
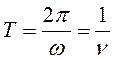−период колебаний; 
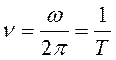− частота волны.
Сферическая волна −волна, волновые поверхности которой представляют сферические поверхности.
Уравнение сферической волны: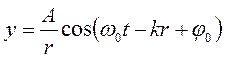 
, где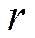 
− расстояние от источника до точки среды, колебания которой рассматриваются.
Скорость, с которой распространяется возмущение в упругой среде, называют скоростью волны* Она определяется упругими свойствами среды. Расстояние, на которое распространяется волна за время, равное периоду колебаний в ней (Г), называется длиной волны.
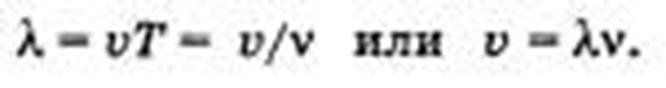
Свободные затухающие колебания. Диференциальное уравнение для свободно затухающих колебаний и его решение. Время релоксации. Логарифмический декремент затухания.
Свободные затухающие колебания − колебания, амплитуда которых уменьшается с течением времени вследствие потерь энергии колебательной системой.
Дифференциальное уравнение свободных затухающих колебаний: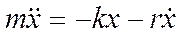 
или 
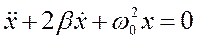, где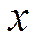 
− смещение тела из положения равновесия; 
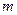− масса материальной точки, совершающей колебания под действием квазиупругой силы 
; 
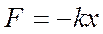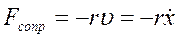− сила сопротивления; 
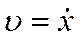− скорость материальной точки; 
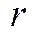− коэффициент сопротивления; 
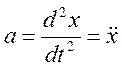− ускорение материальной точки; 
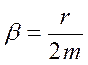−коэффициент затухания; 
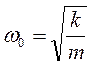− циклическая частота собственных незатухающихколебаний.
Время релаксации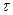 
− промежуток времени, в течение которого амплитуда колебаний уменьшается в 
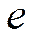раз: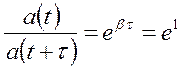 
, т.е. 
.
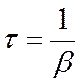Логарифмический декремент затухания: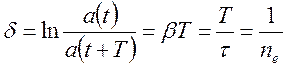 
, − величина, обратно пропорциональная количеству колебаний 
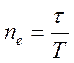, которое совершит система за время 
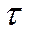, в течение которого амплитуда колебаний уменьшается в 
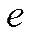раз.
Сложение одинаково направленных гармонических колебаний с одинаковыми частотами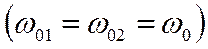 
.
Если складываются два гармонических колебания одного направления и одинаковой частоты
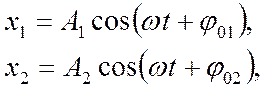
то уравнение результирующего колебания (которое также является гармоническим):
.
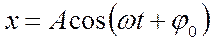Амплитуда и начальная фаза результирующего колебания
,
,
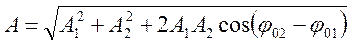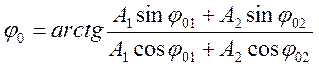где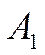 
и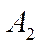 
− амплитуды складываемых колебани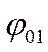й; 
и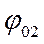 
− начальные фазы складываемых колебаний.
