1. Способ вычисления обратной матрицы с помощью алгебраических дополнений.
Алгоритм вычисления:
1) вычисляют определитель матрицы det A;
2) для каждого элемента 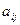 вычисляют алгебраические дополнения
вычисляют алгебраические дополнения 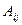 ;
;
3) составляют матрицу 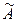 из алгебраических дополнений:
из алгебраических дополнений:
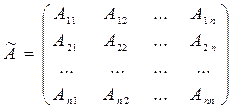 ;
;
4) транспонируют матрицу 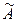 :
:
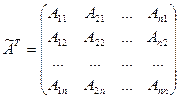
Матрица 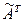 называется присоединенной к матрице А;
называется присоединенной к матрице А;
5) определяют обратную матрицу по формуле:
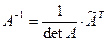 .
.
Пример. Найти матрицу, обратную к матрице 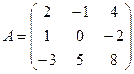
1) det A=0+20-6-0+20+8=42
2) 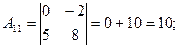
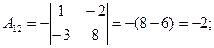
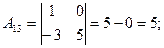
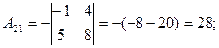
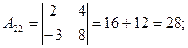
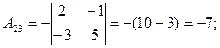
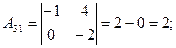
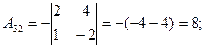
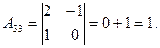
3) 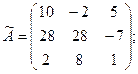
4) 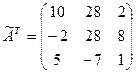 ;
;
5) 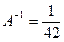
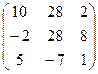 .
.
Сделаем проверку, убедимся, что полученная матрица искомая:
А·А-1= 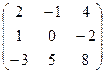
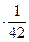
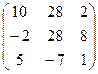 =
= 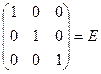 .
.
2. Метод Гаусса вычисления обратной матрицы.
1) припишем к матрице А единичную матрицу того же порядка:
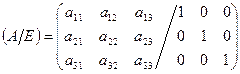 .
.
С помощью элементарных преобразований приведем матрицу 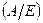 сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица
сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица 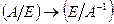 .
.
Пример. 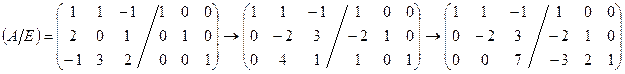
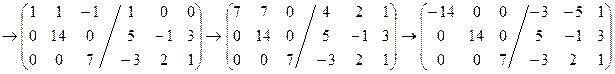
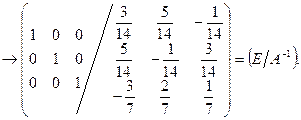 Итак,
Итак, 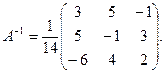
 2015-01-21
2015-01-21 717
717








