Системы линейных уравнений. Рассмотрим систему m уравнений с n неизвестными

Рассмотрим систему m уравнений с n неизвестными

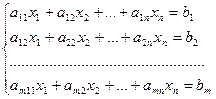(1)

Матрица А, составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1):

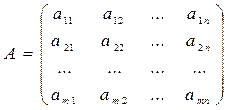
Матрица 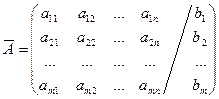называется расширенной матрицей.

Вектор 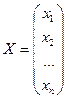называется вектором неизвестных, вектор 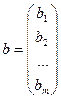называется вектором свободных членов.

Матричная запись системы (1) имеет вид:

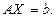
Если вектор b=0, то система называется однородной, если b≠0 (хотя бы один из элементов отличен от нуля), то система называется неоднородной.

Решением системы (1) называется такой вектор X= 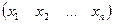, что при подстановке чисел 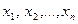в систему (1) получаются верные равенства (тождества).

Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.

Две системы называются эквивалентными, если множества их решений совпадают. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей