Пример 1. Дана система 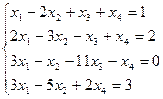
Прямой ход метода Гаусса. Приведем расширенную матрицу системы к ступенчатому виду:
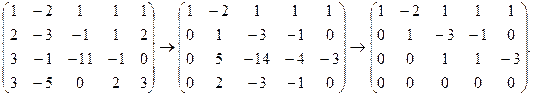
Здесь 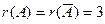 , система совместна.
, система совместна.
Запишем эквивалентную ступенчатую систему:
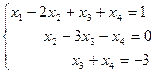
Переменные 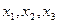 являются зависимыми, а
являются зависимыми, а 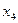 - свободной переменной.
- свободной переменной.
Обратный ход метода Гаусса. Выразим зависимые переменные через свободные, получим:
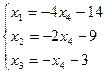 .
.
Пример 2. Решить систему уравнений методом Гаусса
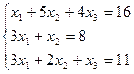 .
.
Составим расширенную матрицу и приведем ее к ступенчатому виду:
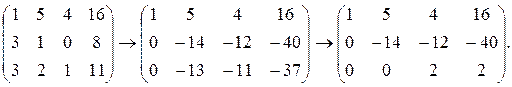
Запишем эквивалентную ступенчатую систему:
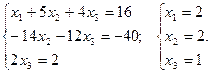
Таким образом, решением данной системы уравнений является вектор 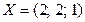 .
.
 2015-01-21
2015-01-21 444
444








