2015-01-21
603
1. Два вектора равны, если их координаты равны.
2. При сложении векторов, заданных в координатной форме, их координаты складываются.
3. При вычитании векторов, заданных в координатной форме, их координаты вычитаются.
4. При умножении вектора на число надо все его координаты умножить на это число.
5. Скалярное произведение векторов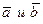 
, заданных в координатной форме, определяется числом вида
.
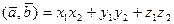6. Векторное произведение векторов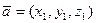 
и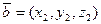 
в координатной форме вычисляется следующим образом:
.
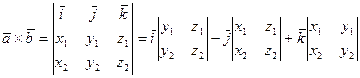7. Смешанное произведение в координатной форме вычисляется следующим образом:
.
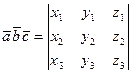Пример 1. Даны два вектора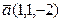 
и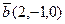 
. Найти косинус угла между векторами 
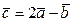и 
.
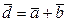Решение. Найдем координаты векторов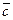 
и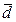 
:
;
.
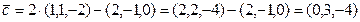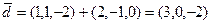Вычислим длины векторов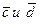 
:
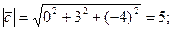
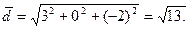
Вычислим косинус угла 
между этими векторами:
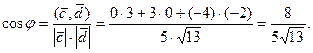
Пример 2. При каком значении 
векторы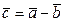 
и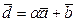 
перпендикулярны (ортогональны)? (Координаты векторов 
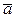и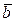 
заданы в примере 1).
Решение. Найдем координаты векторов 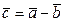и :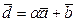
.
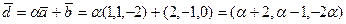Запишем условие ортогональности полученных векторов:
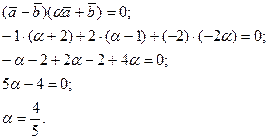
Пример 3. Найти площадь треугольника, построенного на векторах 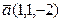и .
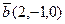Решение. Вычислим векторное произведение векторов 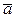и :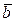
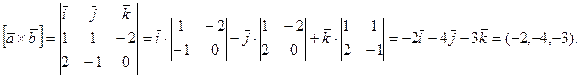
Вычислим модуль векторного произведения по формуле: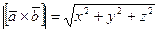 
.
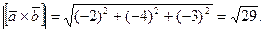
Площадь треугольника равна половине площади параллелограмма
