Определение. Векторным произведением векторов 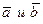 называется вектор
называется вектор 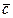 , удовлетворяющий следующим условием:
, удовлетворяющий следующим условием:
1) 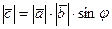 , где
, где 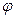 - угол между векторами
- угол между векторами 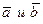 ;
;
2) 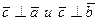 , то есть вектор
, то есть вектор 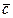 перпендикуляр плоскости, «натянутой» на векторы
перпендикуляр плоскости, «натянутой» на векторы 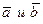
3) векторы 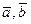 и
и 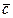 (после их приведения к общему началу) ориентированы по отношению друг к другу, соответственно, как орты
(после их приведения к общему началу) ориентированы по отношению друг к другу, соответственно, как орты 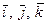 , т.е. образуют так называемую «правую» тройку векторов.
, т.е. образуют так называемую «правую» тройку векторов.
Векторное произведение 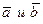 обозначается так:
обозначается так: 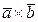 или
или 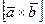 .
.
Свойства векторного произведения
1) 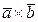 =-
=- 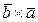 , т.е. векторное произведение не обладает переместительным свойством, то есть при перестановке сомножителей векторное произведение меняет направление;
, т.е. векторное произведение не обладает переместительным свойством, то есть при перестановке сомножителей векторное произведение меняет направление;
2) 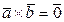 , если
, если 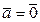 или
или 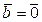 , либо
, либо 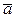 ǁ
ǁ 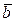 ;
;
3) 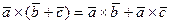 - распределительный закон;
- распределительный закон;
4) 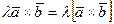 - сочетательный закон по отношению к скалярному множителю;
- сочетательный закон по отношению к скалярному множителю;
5) 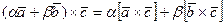 - линейность по первой компоненте. Аналогично, справедлива линейность и по второй компоненте.
- линейность по первой компоненте. Аналогично, справедлива линейность и по второй компоненте.
Модуль векторного произведения (длина вектора 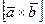 численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 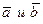 ).
).
 2015-01-21
2015-01-21 565
565








